Rectas Secantes – Qué son y Significado

¿Te has preguntado alguna vez qué son las rectas secantes? ¿Tienes ciertas dudas sobre el significado de este término? En ese caso, has llegado al lugar adecuado. En doncomos vamos a explicarte qué son y cuál es el significado de las rectas secantes. A partir de ahora no volverás a tener problemas para comprender qué significa este término.

Qué son las rectas secantes

Si te fijas el término “rectas secantes” está compuesto por dos palabras: rectas y secantes. Para entender este término es necesario aclarar ambos conceptos.

• Recta. Las rectas en geometría están compuestas por una sucesión de puntos que no tienen fin. Es decir, que son infinitas y carecen de inicio o de final. Junto con el plano y el punto las rectas son conceptos geométricos básicos. Para que una línea sea considerada una recta ha de cumplir las siguientes premisas:
  • Ha de estar creada por una sucesión de puntos que jamás terminan. Es decir, que son infinitas.
  • Todos estos puntos que conforman una recta han de avanzar siempre hacia la misma dirección.
  • Las rectas son unidimensionales. Es decir, solo tienen una dimensión. La dimensión que tienen es la de la longitud.
  • Se determinan por medio de dos puntos.
• Secante. El término secante en geometría hace referencia a la línea o superficie que interseca con otra línea o superficie.

Ahora que sabemos qué significan estos términos en geometría será más sencillo comprender qué es una recta secante. Una recta secante es aquella que corta o bien a una curva o bien a una recta diferente. Para que se consideren secantes han de disponer de un punto en común. El punto en común entre ambas rectas o entre la recta y la curva es aquel lugar en el que se cortan o se cruzan. En el caso de que la recta secante corte una curva puede hacerlo en uno o en varios puntos de la misma. Todo depende de por dónde corte la curva.

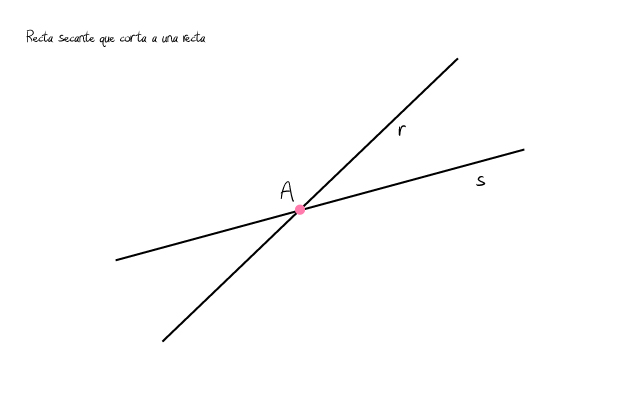
Si te fijas en el ejemplo bajo estas líneas tenemos una recta secante, la recta r, que corta a la recta s. Estas dos rectas se cortan en un único punto que es el punto A.

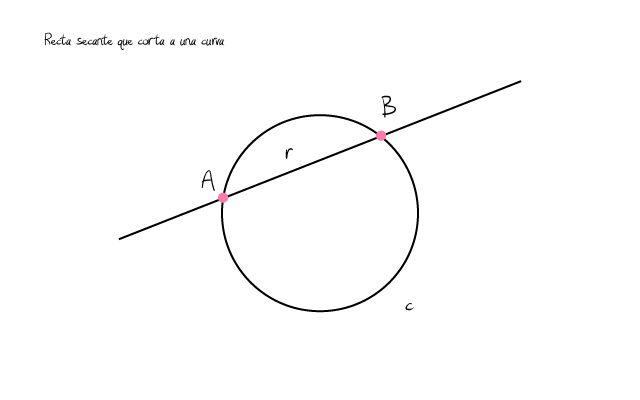
Si te fijas en este nuevo ejemplo bajo las líneas de texto verás que tenemos una recta secante, la recta r, que se encarga de cortar una curva, la curva c. Como se trata de una circunferencia la recta y la curva se cruzan en dos puntos. El punto A y el punto B

Si estas rectas no disponen de ningún punto en común, y, sin embargo, se encuentran en el mismo plano, estaremos ante rectas paralelas. Puedes conocer más datos sobre las rectas paralelas en el artículo de doncomos sobre rectas paralelas.

Las rectas paralelas y las rectas secantes pueden convivir en un mismo plano. De hecho, dentro de la geometría euclidiana se usan de forma habitual para poder resolver muchos ejercicios prácticos e incluso problemas.

En caso de que existan dos rectas paralelas que sean cortadas por una secante se crearán ángulos diferentes. Dependiendo del tipo de ángulo que se creen una vez la secante corte las rectas paralelas, los ángulos que se crean serán de una u otra tipología. Lo normal cuando las rectas paralelas son cortadas por una recta secante es que puedan surgir o nacer alguno de los siguientes ángulos:

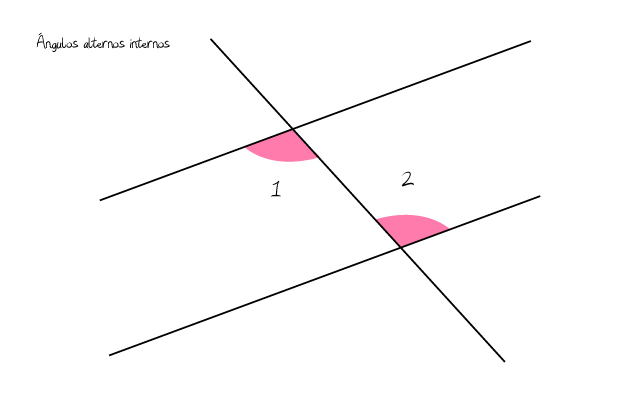
• Ángulos alternos internos. Se consideran ángulos alternos internos aquellos que nacen entre las líneas paralelas que con cortadas por otra recta. Estos se generan en lados diferentes y son iguales.
• Ángulos opuestos al vértice. Los ángulos opuestos la vértice son aquellos que son iguales, y como su nombre indica, opuestos por el vértice.
• Ángulos alternos externos. Los ángulos alternos externos son parecidos a los ángulos alternos internos. Se crean cuando una recta corta dos rectas paralelas. En vez de surgir en la parte interior de las líneas paralelas surgen en la exterior. Estos nacen en lados diferentes de la paralela y de la recta que las corta. Igual que con los ángulos alternos internos los ángulos alternos externos son iguales.
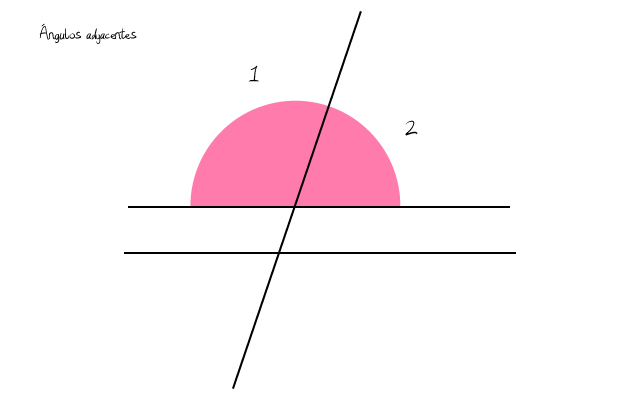
• Ángulos adyacentes. Estos ángulos se caracterizan por tener uno de sus lados en común además del vértice. El otro de los lados que componen estos ángulos son semirrectas opuestas.
• Ángulos correspondientes. Los ángulos correspondientes nacen cuando dos rectas paralelas son cortadas por una recta transversal. Se consideran correspondientes los 8 ángulos que surgen de este corte.
• Ángulos colaterales externos e internos. Los ángulos colaterales externos nacen, al igual que el resto de los ángulos que hemos estudiado, cuando una recta secante corta dos paralelas. En total se crean 8 ángulos al realizarse este corte. Dependiendo de la posición que ocupen estos ángulos serán considerados colaterales externos o colaterales internos. Cuando los ángulos se localizan dentro de la recta, y siempre en el mismo lado de la secante, estaremos ante ángulos internos. Sin embargo, si se encuentran en la parte exterior de la recta, y del mismo lado que la secante, estaremos ante ángulos externos.

Clasificación de las rectas secantes según su forma

Las rectas secantes se pueden clasificar en diferentes tipos según su forma. En concreto, dependiendo de la forma, podremos encontrar las siguientes tipologías:

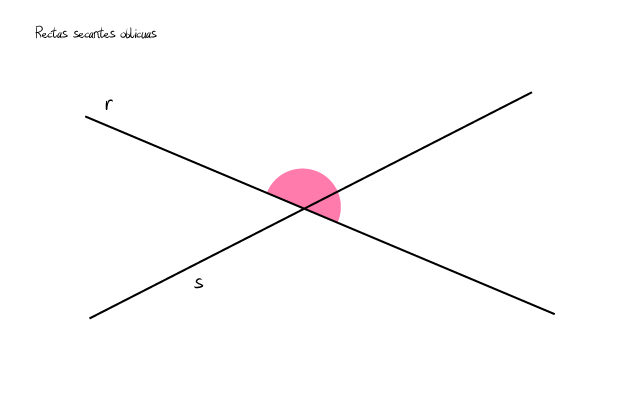
• Rectas oblicuas. Cuando una recta secante corta a otra recta hay un punto en común entre ambas. Gracias a este punto hablamos de que se trata de rectas secantes. Pero al cortarse pueden ser o bien oblicuas o bien perpendiculares. En caso de que se corten en un punto creando ángulos que no son iguales nos encontraremos ante rectas secantes oblicuas.
• Rectas perpendiculares. Ahora bien, en caso de que una recta secante corte otra recta y al cortarse se creen 4 ángulos rectos o de 90º, estaremos ante rectas secantes perpendiculares o bien rectas perpendiculares. Si quieres saber más sobre las rectas perpendiculares puedes echar un vistazo al artículo de doncomos sobre este tema.

En caso de que las rectas se encarguen de cortar una curva o circunferencia nos encontraremos ante los siguientes tipos:

• Rectas secantes. Si la curva o la circunferencia se ve cortada en dos puntos diferentes estaremos ante una recta secante. Dentro de la geometría y de las matemáticas este tipo de rectas son conocidas como una recta secante a una curva.
• Rectas tangentes. Sin embargo, si la recta que corta la circunferencia o curva lo hace en un único punto estaremos ante una recta tangente y el punto de corte será denominado punto de tangencia.

Aquí tienes un ejercicio con rectas secantes

Vamos a ver si verdaderamente hemos comprendido qué son las rectas secantes. Para ello te proponemos realizar el siguiente ejercicio. Ya verás como te resulta muy sencillo averiguar la solución. No obstante, si ves que te atascas y no sabes cómo seguir, no te preocupes. Hemos habilitado un espacio con las soluciones para que puedas resolver los problemas. De esta manera podrás comprobar si tus resultados son correctos o averiguar cuál era la solución del problema. ¿Te apetece comenzar? En ese caso, ¡vamos a por ese problema!

• Ejercicio 1. María y Pablo están comenzando a estudiar en sus clases de matemáticas datos relativos a las rectas. En este momento se encuentran repasando el divertido mundo de las rectas secantes. Su profesor de matemáticas ha querido retarles a crear un ejemplo práctico para comprobar si realmente saben lo que es una recta secante. Para ello les ha pedido que hagan un dibujo de una ciudad con carreteras en el que algunas de los calles formen rectas secantes.

Como a María y Pablo les cuesta un poco entender la diferencia entre las rectas secantes y el resto de rectas, su profesor ha tenido una idea. Ha decidido enseñarles fotos de elementos del día a día donde podemos encontrar rectas secantes. Las fotos que el profesor de María y Pablo les ha enseñado son las siguientes. ¿Sabrías decirnos cuáles de estas rectas son secantes y cuáles no?

Foto 1 ¿Qué tipo de rectas puedes ver?

Foto 2 ¿Qué tipo de rectas puedes ver?

Foto 3 ¿Qué tipo de rectas puedes ver?

Foto 4 ¿Qué tipo de rectas forman las columnas?

Solución al ejercicio con rectas secantes

• Ejercicio 1. El profesor de María y de Pablo propuso un reto a estos dos niños. Dibujar una carretera en la que se encontraran rectas secantes. Para ayudar a los niños a ser capaces de hacer este ejercicio les enseñó varias fotos de nuestro mundo donde las rectas secantes están incorporadas. Pero mezcló estas rectas con otros tipos de rectas. En total les ofreció 4 fotos. ¿Has logrado averiguar cuáles eran rectas secantes y cuáles no? Si quieres saber con certeza cuál es la respuesta correcta… ¡sigue leyendo!

Foto 1. Recta secante

Foto 2. Rectas paralelas… y rectas secantes. Si te fijas El cuerpo del señor corta las líneas del suelo creando con su figura rectas secantes.

Foto 3. Rectas paralelas… y rectas secantes. Las líneas que forman el suelo son paralelas. Sin embargo, las líneas que forman la barandilla se cortan creando rectas secantes.

Foto 4. Rectas paralelas. Si te fijas las columnas no se cortan entre sí. Y además son equidistantes. Por tanto son rectas paralelas.

Te animamos a que, igual que María y Pablo, realices un plano de una ciudad con calles que formen rectas secantes. Puedes divertirte y añadir todo tipo de rectas. Además de las secantes también puedes incluir rectas paralelas. Igualmente puedes hacer ángulos diferentes en función del tipo de corte que hagan las rectas secantes. Tus padres podrán ayudarte a resolver este problema y confirmar contigo si has elegido bien las rectas.

Si te ha gustado este artículo sobre las rectas secantes

Si has llegado hasta aquí, y te ha gustado el artículo sobre las rectas secantes, estamos seguros de que te podrán resultar interesantes los siguientes contenidos de doncomos. Podrás encontrarlos dentro del apartado Matemáticas de nuestro blog, o bien pinchando sobre el propio enlace. 

Si quieres compartir con nosotros y el resto de lectores tus conocimientos sobre las rectas secantes puedes hacerlo a través del apartado de comentarios. Igualmente si tienes alguna duda sobre este tipo de rectas puedes indicarlo en este mismo apartado. Los lectores te ofrecerán sus propios consejos y soluciones para poder resolver tus dudas.

Si te apetece hacer ejercicios personalizados y retar al resto de lectores a resolverlos, no lo dudes y cuélgalos en este mismo apartado.

Si estás contento con este artículo dale a “sí”. Así sabremos que te hemos ayudado a despejar tus dudas y hacer que la geometría resulte mucho más sencilla para ti.