Rectas Perpendiculares – Qué son y Significado

No nos engañemos. A veces entender los principios de la geometría puede resultar un auténtico fastidio. Sin embargo son conocimientos que hay que adquirir y que nos ayudarán a comprender mejor las cosas que nos rodean. Puede que no seas un hacha en matemáticas. Puede que la geometría no sea tu fuerte. Pero gracias a doncomos vas a comprender mejor el concepto de rectas perpendiculares. En este artículo queremos ayudarte a entender qué son las rectas perpendiculares. Trabajaremos también sobre su significado. De este modo no volverás a tener dudas sobre este concepto y sabrás aplicarlo a la perfección. Pero para entender bien qué son las rectas perpendiculares antes hay que explicar qué es una recta.

Recta

Cuando hablamos de rectas nos referimos a una sucesión de puntos que es infinita. Debido a esta característica las rectas no tienen un comienzo ni un final. Pero siempre avanzan hacia la misma dirección. La recta es uno de los elementos geométricos fundamentales junto con el punto o el plano. La recta se caracteriza por lo siguiente:

• Su carácter infinito compuesto por una sucesión de puntos.
• El hecho de que siempre avanza hacia la misma dirección.
• Que están compuestas de una única dimensión y esta es la longitud.
• Que están determinadas por dos puntos.

Qué son las rectas perpendiculares. Significado

El término rectas perpendiculares proviene del latín. En concreto de la palabra perpendicularis. Dentro de la geometría se entiende que las rectas perpendiculares son aquellas que en algún momento, y dentro del mismo plano, se cortan entre sí. Al cortarse crean 4 ángulos rectos e iguales. Ya que los 4 ángulos son de 90º.

Igual que sucede con las rectas perpendiculares, los planos y los semiplanos también pueden ser perpendiculares entre sí si se cortan en 4 ángulos rectos.

Al igual que sucede con las rectas paralelas, las rectas perpendiculares tienen (o no) diferentes propiedades. De este modo pueden ser:

• Rectas perpendiculares simétricas. Decimos que tienen una propiedad simétrica cuando una recta es perpendicular a otra recta. De este modo, si la recta A perpendicular a la B, la B también es perpendicular a la A. A esta propiedad se la llama simétrica.
• Propiedad reflexiva en las rectas perpendiculares. Una recta nunca puede ser perpendicular a sí misma. ¿Por qué es así? Porque una recta jamás puede cortarse a sí misma en un ángulo de 90º. En este caso diremos que la recta también tiene una propiedad reflexiva.
• Propiedad transitiva en las rectas perpendiculares. Igual que sucede en el caso anterior, una recta perpendicular nunca puede ser transitiva. ¿Qué significa esto? Pongamos un ejemplo para entenderlo. Pensemos en un plano en el que se encuentran 3 rectas. Si la recta A es perpendicular a la B y la B es también perpendicular a la C, no se cumple que la C sea perpendicular a la A o viceversa. Estas rectas no pueden ser transitivas. Han de cortarse entre sí y formar ángulos rectos para considerarse perpendiculares. Por tanto, como la recta A y la C no se cortan, no pueden ser perpendiculares entre sí.
• Unicidad. La recta que es perpendicular solo puede pasar por un punto del plano.

Por tanto, las propiedades que comparten las rectas perpendiculares son las de simetría y unicidad. Nunca pueden tener propiedades reflexivas o transitivas entre unas y otras.

Cuando se comienza a estudiar las rectas perpendiculares hay que tener cuidado de no confundirlas con las rectas paralelas. Mientras que las primeras se cruzan entre sí formando 4 ángulos de 90 º. Las segundas nunca se cruzan y avanzan de manera infinita equidistantemente. Si lo piensa con detenimiento el símbolo “+” representaría a la perfección las rectas perpendiculares. Por otro lado el símbolo “=” representaría a las rectas paralelas.

Cuál es la condición que se ha de cumplir para que dos rectas sean perpendiculares

Como hemos explicado dos rectas son perpendiculares cuando se intersectan entre ellas y forman 4 ángulos de 90º. Para corroborar que dos rectas son perpendiculares han de cumplirse una de estas dos condiciones:

• La pendiente de una recta debe de ser el recíproco de la otra. Además esta debe de tener el signo contrario. Es decir:
• Otra manera de ver esta condición es que si multiplicas ambas pendientes el resultado ha de ser siempre -1. Es decir

Veamos si hemos comprendido qué condiciones han de cumplirse para que dos rectas sean perpendiculares. Te proponemos que resuelvas el siguiente ejercicio:

Aquí tienes una tabla en la que aparecen varias pendientes. Te retamos a que averigües que pendientes corresponden a rectas que son perpendiculares.

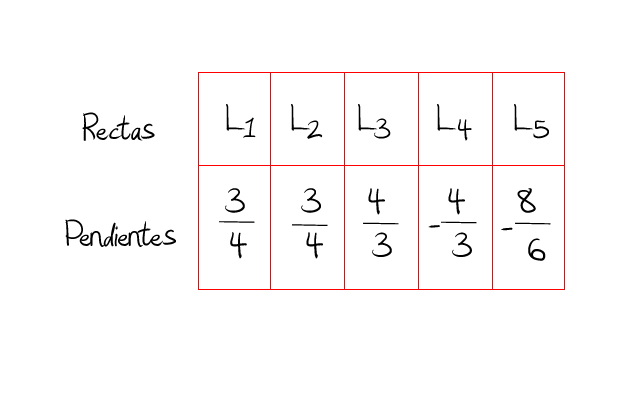
Para resolver este ejercicio necesitamos saber qué parejas son perpendiculares entre sí. Para averiguarlo podemos usar las dos fórmulas que hemos visto unas líneas más arriba. Te las recordamos aquí.

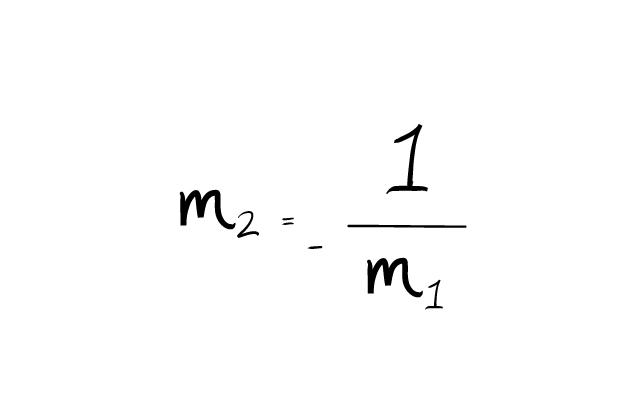
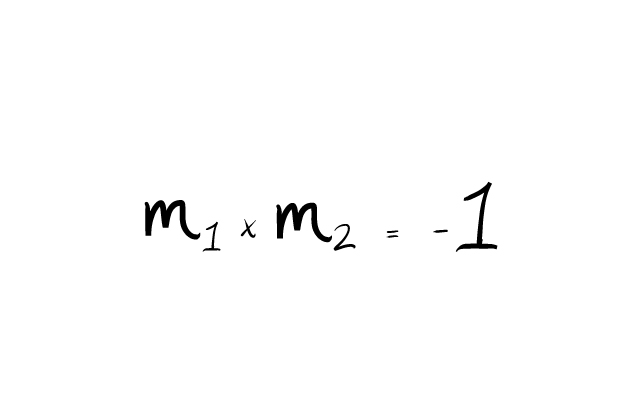
1. En primer lugar vamos a averiguar si las l₁ y la l₂ son perpendiculares entre sí. Para ello usamos la fórmula 2. Aquella por la cual si multiplicamos ambas pendientes el resultado debe de ser -1. Al multiplicarlas comprobaremos que este no es el resultado. Por lo tanto no son perpendiculares entre sí.

2. Ahora procedemos a averiguar si l₁ y la l₃ son perpendiculares entre sí. En este caso podemos ver que al hacer la cuenta nos encontramos con números que son recíprocos entre sí pues están volteados. Sin embargo, además de recíprocos han de tener el signo contrario para que sean perpendiculares. Pero esta segunda variante no se cumple pues al ser ambas positivas el resultado es positivo. Así que aunque a primera puedan parecer recíprocas lo cierto es que no lo son.

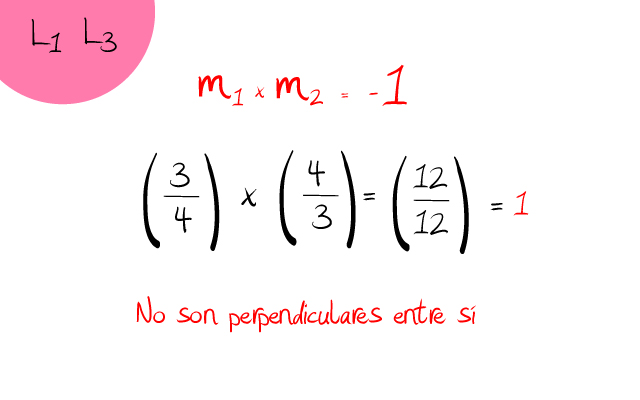
3. Hagamos ahora la misma operación entre la l₁ y la l_4. En este caso las fracciones son recíprocas. Es decir, que están invertidas. Una es ¾ y la otra es -4/3. Además de ser recíprocas una de ellas es positiva y la otra negativa. Por lo que, cuando multipliquemos ambas, se cumplirá parte de la fórmula. Ya que cuando multiplicamos + por – el resultado es negativo. Es decir, -. Una vez multiplicados los signos continuamos con los números. Y al despejar la fórmula como resultado obtenemos -1. Por tanto, la l₁ y la l₄ son perpendiculares entre sí.

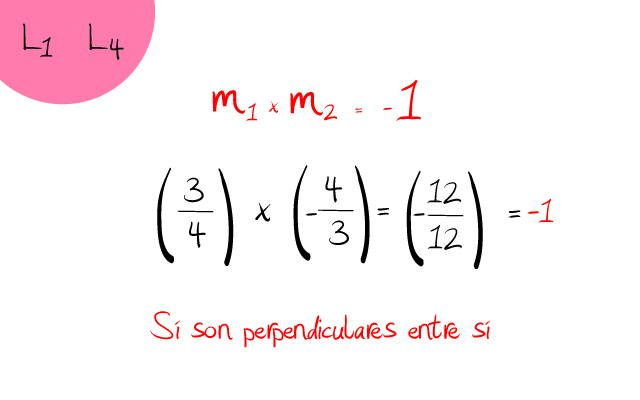
4. Hagamos ahora la misma operación entre la l₁ y la l₅. En este caso las rectas l₁ y l₅ tienen una pendiente de ¾ y -8/6. Aunque inicialmente no se aprecia que sean recíprocas entre sí, sí que podemos observar a simple vista que una de las fracciones es positiva y la otra negativa. Por tanto al multiplicar ambas para despejar la fórmula obtendremos un resultado negativo. Cuando multiplicamos ambas fracciones siguiendo la fórmula m₁ x m₂ = -1 nos encontramos con que el resultado da -1. Por tanto la l₁ y la l₅ son dos líneas rectas perpendiculares entre sí. Otra manera de hacerlo es simplificar la fracción -8/6. Si lo hacemos de esta manera al simplificar serían -4/3. Una vez hecho nos damos cuenta de que es recíproca. Las rectas l₁ y l₅ son perpendiculares también entre sí. Igual que la l₁ y la l₄.
5. Comenzamos a hacer las mismas operaciones con el resto de rectas desde la l₂. Igual que hemos hecho las operaciones con la l₁ y todas las demás rectas, haremos lo mismo con la l₂. Es decir, comprobaremos si las rectas l₂ y l₃, l₂ y l₄ y l₂ y l₅ son perpendiculares entre sí. Para despejar la incógnita actuaremos de igual modo que en los pasos del 1 al 4. Después de realizar las operaciones pertinentes comprobaremos que tanto la l₂ y la l₄ como la l₂ y la l₅ son rectas perpendiculares entre sí. Ya que al despejar la fórmula m₁ x m₂ el resultado en ambos casos es -1. No obstante, si es de un solo vistazo podemos observar que las fracciones de las pendientes son recíprocas y una negativa y otra positiva, no necesitaremos despejar la fórmula. Sabremos de antemano que se trata de rectas que son perpendiculares entre sí.
6. Haremos el mismo ejercicio a partir de la recta l₃. De este modo averiguaremos si la recta l₃ es perpendicular a alguna de las otras rectas. Si observamos las fracciones de las pendientes podemos advertir que en este caso no hay ninguna recta que sea perpendicular entre sí. Las fracciones que quedan no cumplen las dos reglas. Es decir, que sean recíprocas y que una sea negativa y otra positiva. Al no cumplirse ambas reglas es imposible que una vez despejemos la fórmula obtengamos como resultado -1. Por tanto la l₃ y la l₄ no son perpendiculares entre sí. Y la l₃ y la l₅
7. Y por último… l₄ y l₅. En este caso estas dos rectas no son perpendiculares pues ambas son negativas. Además, una vez simplificada la fracción de -8/6 el resultado son -4/3. Igual que la l₄. Como no ambas fracciones no son recíprocas el resultado no puede ser 1. Si despejamos (-4/3) * (-4/3) obtendremos como resultado 16/9. En total obtendríamos 1,77777. Por tanto estas dos rectas no son perpendiculares entre sí.

Seguro que has sabido despejar todas las incógnitas sin tener que leer la explicación que te hemos redactado. Si este es el caso eso significa que ya sabes aplicar las fórmulas sobre la condición para que dos rectas sean perpendiculares. A partir de ahora te resultará muy sencillo saber cómo proceder. Y siempre tendrás claro cuándo dos rectas son perpendiculares entre sí siempre que conozcas su pendiente.

¿Te ha resultado interesante el artículo sobre Rectas Perpendiculares – Qué son y Significado?

Si te ha gustado el artículo sobre qué son las rectas perpendiculares y cuál es su significado, estamos seguros de que te podrán interesar también todos los de nuestra categoría de Matemáticas

Seguro que con ellos aprenderás muchas cosas útiles sobre matemáticas y geometría. Como siempre, si te apetece aportar tu granito de arena sobre las rectas perpendiculares puedes hacerlo a través del apartado de comentarios. Lo encontrarás justo al final de este mismo artículo. Ahí puedes añadir tanto tus conocimientos sobre la materia. Además puedes resolver posibles dudas con el resto de lectores. Es un espacio abierto en el que compartir con los demás tus ideas y conocimientos.

Los redactores de doncomos estaremos encantados de leerte y aprender cosas nuevas. Al igual que el resto de lectores de nuestro blog. ¡Siempre sabemos un poquito más gracias a vuestras aportaciones!

No olvides darle a “me gusta” si te ha resultado interesante este artículo. Así nos ayudas a mejorar nuestro trabajo.

¡Desde doncomos te damos las gracias por leernos!