Cómo dividir fracciones

Si quieres saber cómo dividir fracciones, continúa con la lectura de este artículo, pero antes de entrar en el tema, hablemos un poco de las fracciones.

Las operaciones matemáticas con fracciones vienen desde la antigüedad, se cree que exactamente provienen de los egipcios, pues utilizaban a las mismas para poder resolver los distintos problemas matemáticos que se les presentaban diariamente; las operaciones matemáticas las utilizaban para la construcción de pirámides, para saber cómo distribuían el pan y hasta para estudiar a la tierra como planeta.

Esto ha sido comprobable gracias a evidencias como lo son por ejemplo el papiro de Ahmes; podemos decir que la fracción surge como una forma de medida y a la vez de reparto; los egipcios comenzaron con estas operaciones matemáticas, pero realmente los Indios (India) exactamente en el siglo VI D.C fueron los que instituyeron las reglas de las diferentes fracciones. Las leyes las implantó Aryabhata y más adelante en el siglo VII lo hizo Bramagupta.

Las reglas fraccionarias de hoy en día las crearon en el siglo IX mhavira y en el siglo XII Bháskara respectivamente.

Entonces vemos que las fracciones, o también llamados quebrados, se originaron hace bastante tiempo, incluso Antes de Cristo, son muy remotas. Pues ya eran conocidas por los egipcios, los babilonios y los griegos y surgen como una necesitad de poder medir, contar y repartir.

El nombre de fracción se da porque Juan de Luna fue quien se encargó, en el siglo XII, de traducir al latín el libro de aritmética escrito por «Al-Juarizmi», pues cuando hizo esta traducción, utilizó la palabra Fractio para poder traducir AL-KASR palabra árabe que significa romper o quebrar, de allí que muchos llamen a los fraccionarios números quebrados.

Documento – Papiro de Ahmes

Hablaremos un poco sobre este documento ya que en él se encuentran plasmadas las primeras evidencias de operaciones fraccionarias.

Este documento se encuentra escrito como lo hacían en la época antigua sobre un papiro, éste exactamente tiene de longitud 6 metros y de ancho tiene treita y tres cm; hoy en día sigue conservándose en un buen estado; en él encontramos escritos hieráticos y claro está contenido de tipo matemático; el papiro de Ahmes también recibe el nombre de Papiro de Rhind; la cronología de su contenido se da del 2000 al 1800 A.C; y fue escrito por un escriba llamado Ahmes más o menos en el año 1650 AC.

Este papiro lo encontraron en el siglo XIX, en las ruinas de una de las edificaciones de Luxor, el mismo fue obtenido por Henry Rhind, de allí que también se le conozca con este nombre, fue en el año 1858 DC;  y desde el año 1865 es custodiado por el Museo Británico de Londres. En la actualidad el documento no lo tienen expuesto al público.

En su contenido encontramos exactamente ochenta y siente problemas de tipo matemático, en los cuales se ven vinculados aritmética básica, cálculos de área, progresiones, reglas de tres, ecuaciones de tipo lineal, trigonometría, volúmenes y claro está reparto proporcional y fracciones.

División de las fracciones

Ahora sí entremos en el tema de cómo dividir fracciones; dividir fracciones entre sí puede parecer algo complicado, pero la realidad es que no lo es, pues sólo se trata de invertir cada fracción, luego multiplicar y por último simplificar; continúa leyendo esta guía para que sepas cómo se hace el proceso, verás que no es para nada difícil. También está el método de multiplicar en forma de cruz.

Dividir fracciones multiplicando en cruz

Este método es muy sencillo, lo único que tendrás que hacer es mirar cuál es el numerador de la primera fracción que tengas y multiplicarlo por el denominador de la otra fracción, así te quedará el nuevo denominador, luego miras cuál es el numerador de la segunda fracción y lo multiplicas por el denominador de la primera fracción y de esta manera tendrás un nuevo denominador, mira la imagen que tenemos a continuación.

Si tenemos 4/5 ÷ 5/3 tendremos que multiplicar el nominador 4 de la primera fracción por el denominador de la segunda fracción 3 y obtendríamos el numerador 12, 4×3 =12, así el 12 sería el nuevo nominador, luego tenemos que multiplicar el denominador de la primera fracción, el número 5, por el denominador de la segunda fracción, el número cinco, para obtener así el nuevo denominador 5×5=25, entonces el resultado sería 12/25; como no tenemos un máximo común divisor en el que podamos dividir por los dos números arrojados, no simplificamos y dejamos el resultado así.

Miremos la ilustración

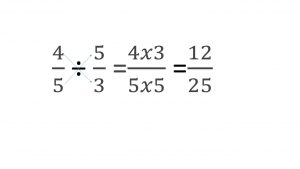
Dividir fracciones invirtiendo

Otro método que tenemos para poder dividir fracciones es la de invertir la fracción para luego multiplicar; para ello lo primero que deberás hacer es invertir la segunda fracción, así si tu segunda fracción es 4/3, cámbiala por ¾; cambia el numerador que tengas por el denominador; una vez hagas esto deberás multiplicar pero en línea, como en el ejemplo que tenemos a continuación.

• Entonces debes dejar la primera fracción tal y como está
• Luego deberás cambiar el signo de división por el de multiplicación.
• La segunda fracción la deberás invertir cambiando el nominador por el denominador, esto se llama hallar el recíproco.
• Luego multiplica los numeradores que te han quedado, o sea los números que están arriba en cada fracción, de este modo obtendrás el nominador del resultado.
• Luego multiplica los denominadores que te quedan, o sea los números de abajo de las fracciones, y así obtendrás el denominador del resultado.
• Deberás simplificar la fracción.

Miremos la ilustración

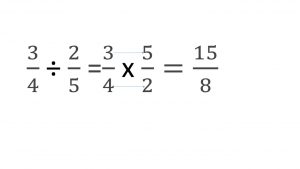
Miremos el siguiente ejemplo

• 3/4÷ 2/5, debes dejar la primera fracción tal como está, o sea el ¾.
• Luego debes cambiar el signo de división por el de multiplicación, así que 3/4÷ 2/5 lo deberás transformar en ¾ x.
• Posteriormente deberás invertir la segunda fracción para encontrar lo que llamamos recíproco, así 2/5 queda en 5/2 y así debes quedar con esta ecuación, ¾ x 5/2.
• A continuación multiplicas los numeradores, los números que están arriba, o sea el 3 y el 5 para obtener el resultado de 15 que viene a ser el nuevo nominador (3 x 5 = 15).
• Luego multiplicas los denominadores, o sea los números que están abajo, que son el 4 y el 2 para así obtener el nuevo denominador que sería el número 8 (4 x 2 =8).
• De este modo obtenemos que el resultado de la división de esta fracción es 15/8, como no tenemos un número natural divisible por los dos números este sería un resultado final.

Nota a tener en cuenta en el momento de dividir fracciones. 

Recordemos un poco como reducir fracciones, aunque creemos que si ya estás buscando como dividirlos, es porque ya sabes hacer esto.

Lo que tienes que hacer es enlistar los factores tanto del numerador como del denominador; los factores son aquellos números que cuando los multiplicamos entre sí obtenemos otro número, entonces los factores son todos los números que cuando los multiplicamos podemos obtener el número que necesitamos, tanto del nominador como del denominador y que al dividirlos dé un número entero.

Comienza a hacer tu lista de números del menor al mayor, debes incluir el número 1 y el número que quieres factorizar. Así  por ejemplo, hagamos la lista de esta fracción 30/15

30: 1, 2, 3, 5, 6, 10, 15, 30

10: 1, 2, 5, 10

Para simplificar esto entonces tendríamos que encontrar el MCD que es el máximo común divisor, o sea el número más grande por el cual se puedan dividir ambas fracciones en este caso sería el 5, entonces la simplificación de la  fracción 30/10 quedaría 6/2.
.