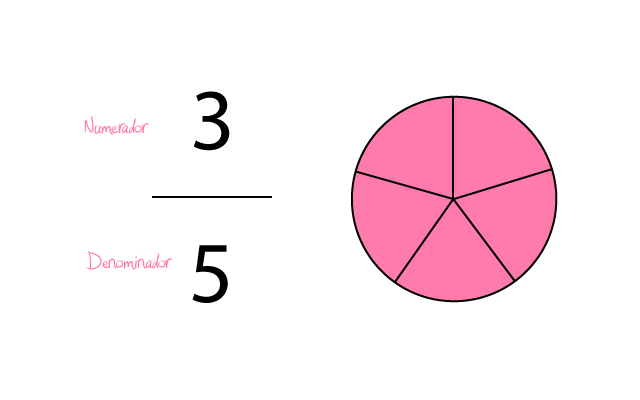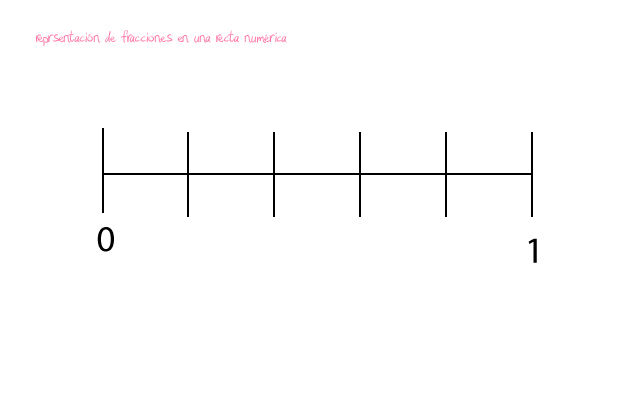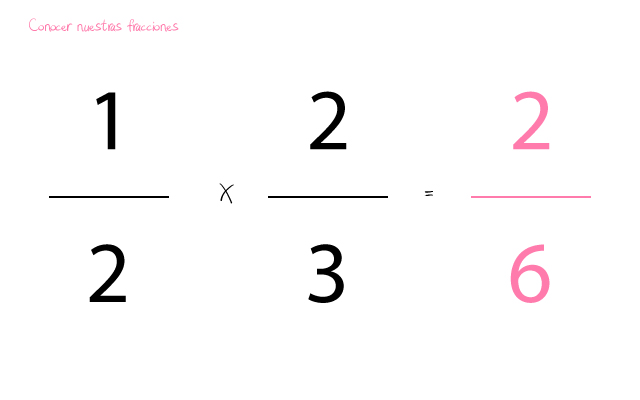Rectas Numéricas con Fracciones – Qué son y Significado

¿Has pensado alguna vez que una recta numérica te puede servir también para añadir fracciones? ¿Sabrías cómo hacerlo? ¿Sabes qué son las rectas numéricos con fracciones y cuál es su significado? En este artículo vamos a explicártelo todo para que salgas de dudas de una vez por todas. ¿Te gustaría aprender a hacer estas rectas? En ese caso, ¡sigue leyendo!

Qué son las rectas numéricas con fracciones. Su significado

Cómo funcionan las rectas numéricas

Antes de empezar a explicar cómo crear una recta numérica con fracciones es importante que comprendamos dos conceptos: el de rectas y el de rectas numéricas. A continuación vamos a explicarte ambos.

Las rectas

Las rectas son líneas unidimensionales compuestas por muchísimos puntos. Son uno de los conceptos elementales dentro de la geometría. Y lo son junto al plano o al punto. Cuando decimos que una recta está compuesta de muchos puntos es porque, si te aproximaras a ella con una lupa, verías que esa línea que observas se compone de muchos puntitos pequeños.

Las rectas se caracterizan por ser infinitas y carecer de principio y de final. Todos los puntos que forman la recta avanzan de manera infinita hacia el mismo lugar.

Muchas personas confunden las rectas con los segmentos o las semirrectas. Sin embargo no son los mismos elementos.

• Los segmentos se caracterizan por comenzar en un punto y acabar en otro. Luego no son infinitos como las rectas. De hecho los segmentos son una parte finita de las rectas.
• Las semirrectas, por su parte, se caracterizan por tener principio pero no fin.

Este equívoco suele estar relacionado con la forma de representar las rectas cuando se estudian. Como normalmente se dibujan sobre una pizarra o papel se les da una forma finita. Sin embargo hay que recordar que no son finitas, sino infinitas. De esta manera evitaremos liarnos.

Las rectas numéricas

Cuando hablamos de una recta numérica lo que hacemos es unir dos conceptos diferentes en una única representación. En esta recta hallaremos números separados entre sí a la misma distancia. El aspecto de una recta numérica es muy similar al de la regla que se usa en dibujo técnico. Compuesta por líneas verticales que atraviesan la recta y que marcan el número.

Las rectas numéricas con fracciones

Las rectas numéricas se representan con números enteros tanto positivos como negativos. Sin embargo también se pueden incluir fracciones. En caso de incorporar fracciones a la recta estaríamos hablando de rectas numéricas con fracciones.

Cómo crear una recta numérica con fracciones

La principal duda que nos surge cuando trabajamos con fracciones en las rectas numéricas es cómo colocar dichas fracciones sobre ellas. Vamos a explicarte a continuación cómo se hace:

Colocar una fracción en la recta numérica

Lo primero que vamos a aprender es cómo se coloca una fracción en la recta numérica. Verás que con estos 5 sencillos pasos que vamos a explicarte te resultará súper rápido averiguar cómo hacerlo. Vamos a ellos.

1. Conocer nuestra fracción. Para posicionar las fracciones en la recta numérica debemos de pensar en una fracción. Por ejemplo 3/5.
2. Observar nuestra fracción. La fracción nos indica el número de partes en las que se divide un entero. ¿Por qué esto es así? Porque las fracciones forman parte de un entero.
3. Dibujar la recta. En este caso de 0 a 1 habrá 5 partes. Es como si tuviéramos un círculo dividido en cinco quesitos. El círculo sería nuestro entero y cada quesito las fracciones que lo conforman.
4. Dividir la recta. Por tanto ahora tenemos que dividir la recta en 5 partes iguales. Las partes en las que dividimos la recta nos las da el denominador de la fracción de la que hemos partido. Recuerda que las fracciones se dividen en dos partes. El numerito de arriba, que se llama numerador, y el de abajo, que se considera denominador. Mientras que el denominador nos va a indicar el número de partes en el que se divide la recta, el numerador nos va a indicar la posición exacta que ocupa dentro de ella.
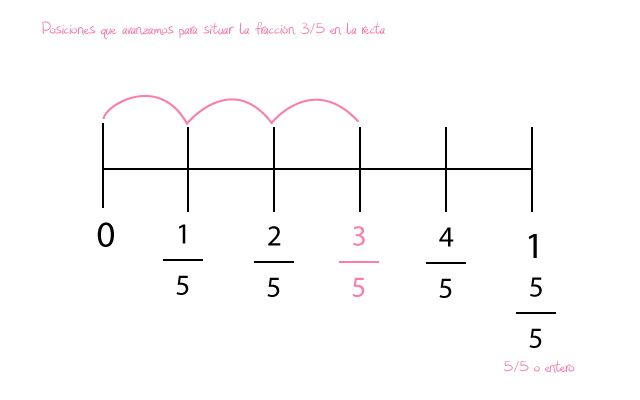
5. Colocar la recta en la posición adecuada. Si nuestra fracción es 3/5, deberemos de avanzar tres posiciones por nuestra recta. Esta posición será la de 3/5. Ese es precisamente el lugar donde se ubica nuestra fracción. En este caso nuestra fracción es 3/5.

Colocar dos fracciones con diferente denominador en una recta numérica

Ahora hagamos el ejemplo un poco más complicado sobre cómo colocar las fracciones en una recta numérica. Imagina que tienes dos fracciones con diferentes denominadores y quieres colocarlas en la misma recta. ¿Cómo deberías de colocarlos en el mismo entero de tu recta numérica? ¿Es posible? Veámoslo a continuación.

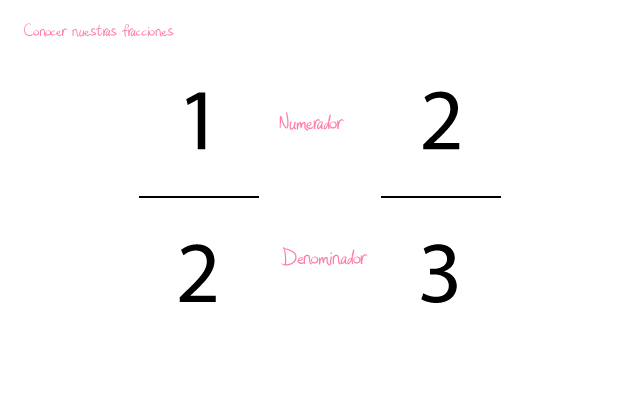
1. Conocer nuestras fracciones. En este caso las fracciones con las que vamos a operar tienen numeradores y denominadores diferentes. Jugaremos con dos fracciones sencillas. ½ y 2/3.
2. Hacer una multiplicación de fracciones. Para saber qué posición ocupan dentro del mismo entero es necesario hacer una multiplicación de fracciones. Ya verás que es muy sencillo. ¡Aunque a primera vista no lo parezca! Para ello multiplicaremos cada numerador con el otro y cada denominador con el otro denominador. ¿Sabes cuánto sería el total? ¡Efectivamente!, 2/6. También puedes sacar el mínimo común múltiplo para averiguar esta cifra.
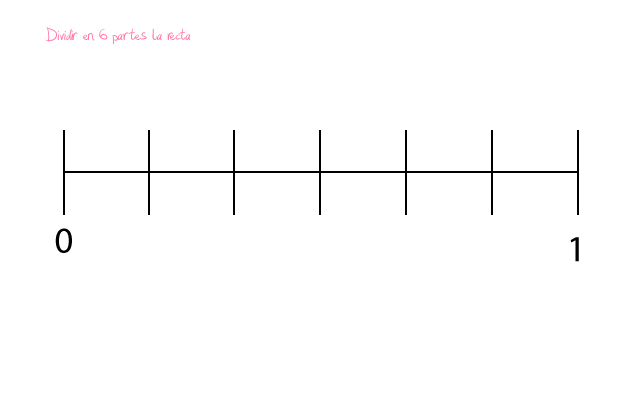
3. Prestar atención al denominador. Una vez hecha la multiplicación de fracciones el denominador nos marca las posiciones que tendrá nuestra recta numérica. Es decir, el número de separaciones equidistantes que hay entre cada número. El total es de 6.
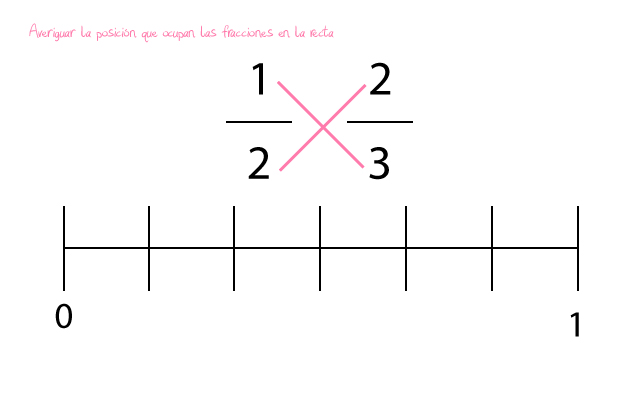
4. Averiguar en qué posición va cada una de las fracciones en la recta numérica. Vayamos al meollo de la cuestión. Averigüemos qué posición ocupa cada una de nuestras fracciones dentro de la recta. Para saberla tendremos que multiplicar el numerador de cada fracción con el denominador de la otra fracción que tenemos. Es decir, que multiplicaremos el 1 con el 3 y el 2 con el 2.
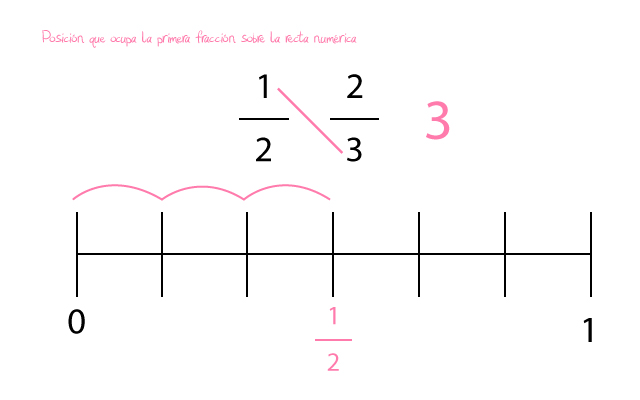
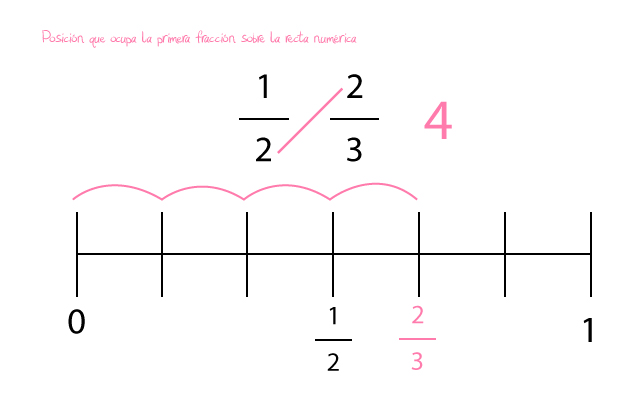
5. Posición que ocupa la primera fracción en la recta numérica. Al multiplicar el numerador de la primera fracción con el denominador de la segunda fracción obtendremos un total de 3. Este es el número de espacios que nuestra fracción ½ debe de avanzar por la recta. Y esa es la posición que ocupará dentro de nuestro entero la fracción ½.
6. Posición que ocupa la segunda fracción en la recta numérica. Del mismo modo que hemos procedido con la primera fracción deberemos de proceder con la segunda para averiguar en qué posición de la recta numérica se encuentra. En este caso multiplicaremos el numerador de la segunda fracción con el denominador de la primera. En total obtendremos un 4. Estas son las posiciones que hemos de avanzar sobre la recta. Y este será el espacio que ocupará la segunda fracción dentro de la recta numérica. ¿Te has fijado en que la segunda fracción, la de 2/3, es mayor que la primera, la de 1/3?

Colocar fracciones impropias

En nuestro último ejemplo vamos a averiguar cómo colocar en una recta numérica una fracción impropia. Es decir, una fracción cuyo numerador es mayor que el denominador. Estas fracciones son conocidas como fracciones impropias en la recta numérica. Tranquilo. Ya verás que resulta mucho más fácil de lo que parece a primera vista. Veamos cómo hacerlo.

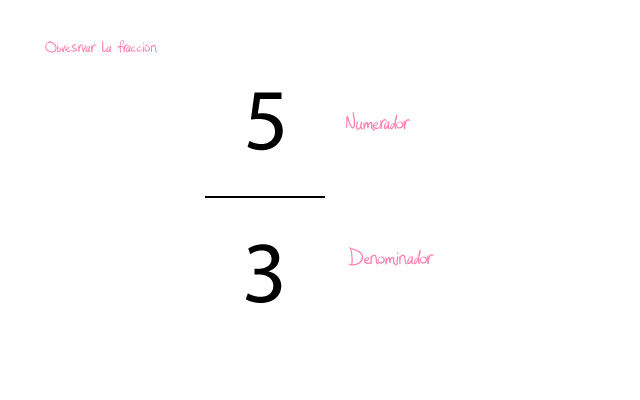
1. Observar la fracción que tenemos. En este caso nuestra fracción con la que vamos a hacer el ejemplo será la siguiente: 5/3. Si te fijas el numerador de esta fracción es superior al denominador.
2. Pasar la fracción impropia a número mixto. Para poder averiguar cómo colocar la fracción impropia debemos de pasarla a número mixto. ¿Sabes cómo se hace esto? Muy sencillo.
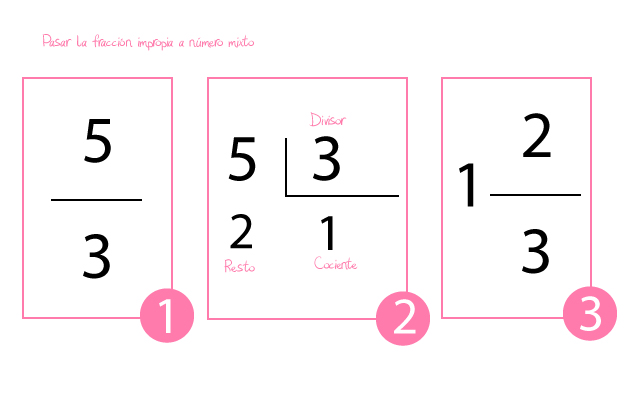
   1. Paso 1. En primer lugar observamos nuestra fracción.
   2. Paso 2. En segundo lugar pasamos a número mixto la fracción. El método para pasar a número mixto una fracción impropia es dividir el numerador de esta fracción por su denominador.
   3. Paso 3. A partir de ahora el cociente de esta división representará al número entero. Cuando hacemos una división nos queda un resto. Pues bien, este resto será el numerador de la fracción. Por su parte el denominador seguirá siendo el mismo que el que tenía la fracción. Es decir, el divisor con el que hicimos la división. Es decir, que el número mixto de la fracción 5/3 será igual a 1 entero y 2/3. Puedes ver la explicación de estos tres pasos en la imagen que tienes a continuación. Verás que de esta manera te resulta mucho más sencillo comprender la operación.
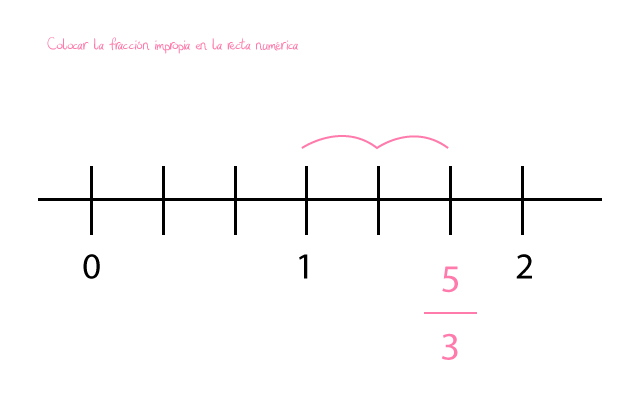
3. Observar el número mixto. El entero que nos ha dado de convertir la fracción en número mixto nos indica la posición en la que se encuentra la fracción. Y la posición es en el entero 1. Es decir, que se ubicará entre el 1 y el 2. Nuestra recta numérica se compondrá por tanto de los segmentos 1 y 2 para poder colocar la fracción.
4. Dividir las partes de cada segmento. Como nuestro denominador del número mixto nos indica que cada entero se divide en tres partes, dividiremos nuestros enteros con ese número de partes. Ahora debemos de colocar la fracción a partir del entero 1 en la posición 2/3. Es decir, que avanzaremos dos posiciones desde el 1. Este será el lugar que ocupa la fracción original. La de 5/3. Y ya habríamos terminado. ¿A que ha sido mucho más fácil de lo que parecía al principio?

Si te ha gustado este artículo sobre qué son las rectas numéricas con fracciones…

Si te gusta conocer más datos sobre el interesante mundo de las matemáticas, de las rectas numéricas o de las fracciones, estás en el lugar adecuado. En doncomos puedes aprender mucho más sobre estos temas en nuestro espacio Matemáticas. Aquí encontrarás información detallada sobre estos aspectos y muchos más que seguro que te resultan interesantes. Hemos escogido algunos artículos que te pueden gustar y con los que aprenderás mucho más. Solo tienes que pinchar sobre el enlace para que te redirija a cualquiera de ellos.

Si quieres compartir tus propios conocimientos sobre las rectas numéricas con fracciones puedes hacerlo en el apartado de comentarios. Lo encontrarás justo al final de este artículo. Este espacio está habilitado para que puedas dar tu opinión u ofrecer más información al resto de lectores. Además puedes proponer retos interactivos a todos los que lean el artículo creando ejercicio sobre rectas numéricas con fracciones.

Si te ha gustado este artículo no olvides darle al sí cuando acabes de leerlo. Tu feedback es muy importante para los redactores de doncomos. De esta manera sabemos si el material didáctico que te ofrecemos te resulta útil o no.

Desde doncomos, como siempre, te damos las gracias por leernos.