Qué es una varianza en estadística

Hoy  traemos  al debate una pregunta aparentemente compleja, que por generaciones  ha  confundido  tanto a  estudiantes como a profesionales, que abarca un concepto fundamental para  nuestros  tiempos, y   ha dejado sin pelos a  más de una cabeza por año, se  atreven a  afirmar gran parte de los  discípulos durante  su  curso por  la facultad. Una pregunta  que  para  variar puede  llevarnos a  una  respuesta  bastante simple, todo depende  de cómo se mire el problema. Como sabemos  que usted  está deseando  conocer  la pregunta  que  tanta expectativa  ha creado, se la  escribimos simplemente,  sin más  preámbulos: ¿Qué es una varianza  en estadísticas?

¿Varianza  Estadística?

Si  usted tiene  más  de  dieciocho años,  tras  leer  esta pregunta seguramente su cuerpo experimentará varios  tipos de  reacciones, una reacción instantánea,  que  no es más que la  sorpresa mezclada con un hormigueo que  desespera  pero resulta controlable. Sobre todo si le ha tocado responder a cómo calcular la varianza alguna vez.

Hoy le proponemos  un  análisis  práctico que  le ayudará a  entender  que  es la  varianza  pero en estadística, lo que  le  será  de  muchas utilidad en la vida, al mismo  tiempo lo  librará de la Alopecia.

Historia de la  varianza y  su  concepto.

El término  varianza lo debemos  agradecer  a Ronald Ficher, que  en una publicación en el año 1918  propone la varianza como “la  mediada  de  las  desviaciones de  una variable, si se considera  el valor medio de  dicha  variable”.

Visto de  otra  manera, la  varianza  es  una  medida  de  dispersión  que refleja, da valor  a  las  variaciones,  a  las  desviaciones, asume  y contabiliza  lo  que  de alguna  manera pudiera  definirse como un posible margen de  errores.

Lo  que más  tiende  a confundir es que en la  teoría de probabilidades,  la  varianza se  entiende como  la Esperanza del cuadrado de la desviación de una variable respecto a su media, y  aunque  el término  Esperanza, utilizado en  un concepto matemático ya  es de por sí bastante inusual,  eso  no  quiere decir que  la  esperanza sea  calculable.  De  seguro usted nunca ha escuchado a  nadie  decir, “Tengo 16.9 esperanzas de  que  me bese” cuando  está  desojando una flor.

Lo más  importante  a valorar  para  entender  este concepto es que   al  contrario  de la  matemática básica, y los  cálculos  convencionales  a los que  usted se ha enfrentado hasta  ahora, las probabilidades  se  basan en el cálculo, lo  más  exacto posible  de la predicción de algún evento  futuro.

Visto de  otra  manera tenemos que  la  matemática  que  usted  ha estudiado hasta el  momento se  basa  en hechos, eventos  y objetos reales, que  existen en el  presente  o fueron pasado, pero que ya  tuvieron lugar y por ello fue  posible  en su  momento, tener una  dimensión  exacta del objeto o fenómeno  a  estudiar, lo que los  hace perfectamente  cuantificables.  Sin embargo  la  teoría  de  las  probabilidades  nos  propone  pensar en al futuro,  y  aquí lanzamos  una nueva  pregunta, ¿Usted sabe lo que  va  a pasar  mañana?

¿Cómo podemos predecir  el error?

El  mundo desde  su  surgimiento  y evolución ha  seguido un desarrollo cíclico, constante  y  periódico, y  aunque  nos referimos  al mundo natural,  a las plantas, las  rocas, la  fauna, entiéndase que  nosotros  no estamos exentos  de ello, y la  prueba  más  fácil  es que  usted  mire  ahora  mismo para  su muñeca izquierda y  se dé cuenta  que  su día, y  toda  su vida  se  basa en pequeños  ciclos de  sesenta  minutos, que  se repiten constantemente  uno detrás del otro.

Es por  esto  que   basados  en  la historia, en el  análisis minucioso de  cada  uno  de estos  ciclos hemos  podido trazar  distintos  modelos o  ecuaciones  matemáticas, que  nos permiten de  alguna  manera tener una  noción,  no del  futuro  en general, sino  de  un evento futuro  específico, el cual seremos  capaces  de  calcular  antes que  suceda, en dependencia de  lo buenos  que  seamos a la hora de hacer el análisis de las probabilidades.

El hecho de  que  pretendamos  cuantificar  o definir  un evento  futuro,  enmarca  la  idea  de que  dicho  evento puede  ser exactamente  tal y como  lo  esperamos  o  similar,  con  algunas  variaciones, y  es ahí  donde  entra  en  el juego  la  varianza, aunque  para  poder  entenderlo mejor aún debemos  valorar otros  conceptos.

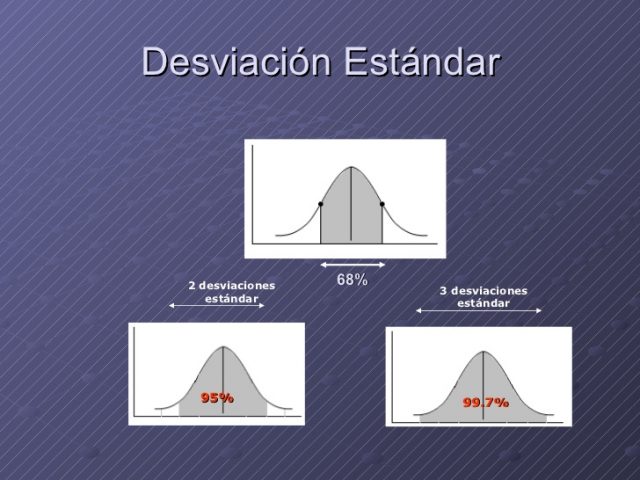
Un concepto muy importante a  la hora  de entender  la  varianza  es la desviación estándar o desviación típica, que representa la magnitud de la dispersión de variables dentro del  intervalo y de razón, pero  como  este  concepto  tal vez resulte un poco abstracto,  hagámoslo un poquito  más  digerible.

Un ejemplo para entender la Varianza Estadística

Usted  pretende  realizar  un análisis estadístico  donde  valorará la posibilidad de que  su  padre  le regale  un Mercedes. Para  ello  la condicionante es que deberá  graduarse con diploma de oro, y para  ello, aparte  de estudiar bastante, deberá  lograr un  promedio acumulado que se comporte  en  el rango establecido para la obtención de dicho título.

Como  usted es una  persona muy precavida  y  a  la vez un excelente  estudiante, se plantea  tres incógnitas  y  las  escribe en  un papel.

1. ¿Cuánto  tengo que  acumular para graduarme con diploma de oro?,
2. ¿Cuál será  la desviación  estándar para  el resultado esperado?,
3. ¿Cuál  será  la  varianza?

Lo primero que  hará  usted es calcular  el resultado acumulado de sus notas hasta  el momento, y ahí sabrá su promedio, o lo que  es lo mismo, la  media  de  sus  evaluaciones.

Luego  deberá  hacer un análisis de  cuantos puntos  debe  subir  o mantener para llegar al valor esperado, lo que lo obligará  a  centrarse  en  algunas  asignaturas  y otras no  tanto, con el propósito  de obtener  su meta, el diploma  de oro que  garantizará “El Mercedes”.

Para garantizar el  diploma usted deberá terminar con un promedio escolar que fluctúa entre un valor mínimo y un valor máximo, que  si los  cuantificamos  de manera hipotética pueden ser 10 puntos de  valor máximo  y 9.5 de valor mínimo.

Aplicando la Estadística

Por tanto usted  se deberá  preparar para terminar  con un acumulado medio de 9.75 puntos,  que  será a partir  de ahora  su resultado esperado, sin embargo, si  termina  con cualquier otro  promedio que  esté  comprendido en el rango entre 10 y 9.5, como por ejemplo 9.6, también obtiene  el diploma  aunque  su resultado sea parecido, pero no  igual  al esperado.

Si aplicamos la estadística a lo anteriormente  expuesto, tenemos que  usted debe  alcanzar en  sus  notas  un valor esperado de 9.75 puntos,  con  una  desviación estándar o típica  de entre 0.25 puntos que  le garantizará el  resultado que  usted  desea,  y  la  varianza será  igual a su desviación  típica  elevada  al cuadrado, pues lo que  hace la varianza es establecer la variabilidad de la variable aleatoria.

Un concepto no tan abstracto

Si después  de  haber  hecho este  razonamiento usted  sigue  con ganas de estirar  su cabello, debe  valorar dos  posibilidades:

1. No  se disguste ni  le  cause  más  preocupaciones  a su  padre, tome  de la  mano su  vida  y sea  considerado,  aunque le resulte doloroso, cambie  el  “Mercedes” por  una  escúter y  salga  a  la  calle, verá como encuentra  un sinnúmero  de  posibilidades de  abrirse  paso en la vida. Un  universo  que no le  exige  calcular   la varianza,  o  la  media,  o la  desviación  estándar, sea feliz.
2. Si aún con el cabello estirado siente que puede, y sobre todo quiere seguir tratando de entender estos conceptos, ¡adelante!, de los cobardes no se ha escrito nada. Para enfrentar este y otros conceptos mucho más abstractos, solo hay que poner mucho empeño y dedicación, recuerde si otros pueden usted también.

Eso sí, si  usted opta por  esta  segunda opción,  no  está  de más  un tratamiento  capilar de  vez en cuando, para evitar un posible daño estético.