Teorema de Pitágoras – Qué es y Ejemplos
Contenido del Artículo
Para muchas personas el tema de las matemáticas resulta difícil, complicado e incluso aburrido. Tal vez porque tienen poco o ningún interés en el tema. Sin embargo, es posible disfrutar de ella si la entendemos bien. Para esto, necesitamos explicaciones sencillas y fáciles de entender; sobre todo si son temas que asustan como el Teorema de Pitágoras.
Si eres uno de los que se hacen la cabra cuando le hablan de números; entonces, ha llegado el momento de tomar cartas en el asunto; que este post te viene como agua de mayo. El teorema de Pitágoras fue uno de los tantos temas de los que se nos habló en nuestras clases de bachillerato (como el calcular el perímetro y el área); que quizás no comprendimos en el momento y que sea por pena, temor o por algún otro motivo, no pedimos a nuestro profesor que volviera a explicar.
El teorema
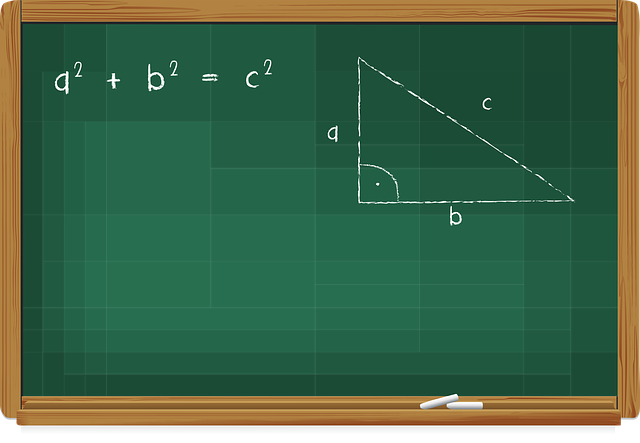
Primero que nada recordemos quién era el fulano Pitágoras. Fue un filósofo y matemático griego que descubrió y demostró que en todo triángulo rectángulo, presenta en el cuadrado de la hipotenusa igual condición a la suma de los cuadrados de sus catetos. A este planteamiento se le conoce como un “teorema”; llamado el de Pitágoras.
En esta breve definición podemos encontrar palabras desconocidas que nos impiden comprender por completo el significado de lo que se nos está diciendo. Es decir, que te quedas en las mismas y no entiendes un pepino. Por ello, es importante que antes de continuar aclaremos lo que significan algunas de ellas.
Retomando el término “teorema”, que suena muy elegante pero que ni idea de lo que es. Cuando hablamos de lo que es un teorema; nos referimos a una propuesta que afirma una verdad que podemos demostrar. En cuanto a un triángulo rectángulo, es aquel que posee un ángulo recto, es decir, de 90º. La hipotenusa, que te puede sonar hasta a insulto; pero no lo es, sería el lado más largo del triángulo, mientras que los catetos son los dos lados restantes.
Instrucciones
Ahora bien, pongámonos serios y vayamos al meollo del asunto. La teoría siempre es la base de la práctica y en eso se ha sustentado todo el avance científico y tecnológico de la humanidad; así que no des lugar a la pereza, pon a funcionar las neuronas con los siguiente ejemplos.
Observa en la siguiente imagen lo antes dicho, utilizando un ejemplo sencillo; ¡vamos a por ello!:
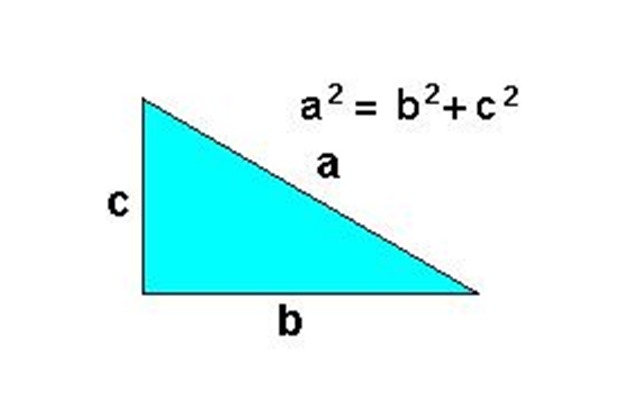
En la gráfica, el lado “a” es la hipotenusa y los lados “b” y “c” son los catetos. La fórmula dice que la hipotenusa al cuadrado es igual a la suma del cuadrado del cateto “b” y el cuadrado del cateto “c”.
Llevemos la misma fórmula a la práctica con otro ejemplo; en el cual sustituiremos las letras por valores reales. Supongamos lo siguiente:
A=?
B=12
C=5
Sabiendo que B es igual a 12 y que C es igual a 5 debemos calcular el valor de A:
A2 = 122 + 52
La raíz cuadrada de 144 es 12 y la de 25 es 5. Si no sabes cómo calcular la raíz cuadrada de los números puedes valerte de una calculadora, lo cual facilita un poco el trabajo. Siguiendo con nuestro ejercicio, este quedaría de la siguiente forma:
A2 = 144 +25
Entonces, ya solo es cuestión de sumar:
144 + 25 = 169
Si buscamos la raíz cuadrada de 169, el resultado será 13. ¡Listo! ¡Lo tenemos! Sabemos el valor de nuestra incógnita. El lado A, es decir, la hipotenusa es igual a 13. No resultó ser tan difícil como lo habíamos pensado, ¿verdad?… Claro, como dice el dicho: la práctica hace al maestro. Por ello, si deseas ser un experto realizando este tipo de ejercicios es vital practicar y, si no te sale a la primera, no pasa nada; no te des por vencido.
Veamos otro ejemplo en donde conocemos los siguientes datos:
A= 3
B=4
C=?
En este caso desconocemos el valor de C, pero es el mismo procedimiento. Sustituyamos las letras por valores numéricos:
32 + 42 = c2
La raíz cuadrada de 9 es 3 y la de 16 es 4. Ahora sería cuestión de sumar:
9 + 16 = 25
Y la raíz cuadrada de 25 es 5 entonces ya tendríamos descifrada la incógnita, el valor de C es 5.
Para que no pases pena haciendo el listo en clases; es importante recordar que este teorema solo puede aplicarse para calcular la longitud de un lado en un triángulo rectángulo.
Que Necesitas
Ahora, ¿de cuánta utilidad es este teorema en nuestra vida si no somos matemáticos o científicos? El teorema de Pitágoras nos permite conocer la longitud del tercer lado del triángulo rectángulo sabiendo previamente las longitudes de sus otros lados.
Por otra parte, podemos utilizarlo en nuestra vida diaria para calcular la distancia en la que se proyecta la sombra de un árbol; conociendo la altura del mismo y la distancia que hay del árbol hasta donde llega la sombra y en otros casos similares.

¿Dirás que quién rayos se divierte calculando las sombras?, pues podría sorprenderte lo interesante que puede ser calcular la longitud de las sombras; sobre todo si piensas en las culturas antiguas. Anteriormente, no existían los relojes, y los antiguos calculaban el tiempo a partir de la longitud de las sombras de los árboles. Entonces, si por casualidad estás de excursión y te has quedado sin batería, calculando la longitud de las sombras podrás hacerte una idea de la hora.
Permítenos contarte algo sobre los Mayas que tiene que ver con esto. Como todos sabemos, ellos eran grandes matemáticos y no existían las calculadoras en la época. Cualquiera observa su habilidad para los cálculos en sus pirámides. Un detalle arquitectónico impresionante en El Castillo de los Mayas construido como homenaje a Kukulcán, es la famosa sombra de la serpiente emplumada.
¿A que no sabías que esta pirámide fue diseñada muy apropósito de los dos equinoccios del año; para que los rayos del Sol proyecten la sombra de la serpiente en los laterales de las escaleras? Entonces, ¿cómo calcularían las longitudes de las sombras los mayas? ¿Ahora te das cuenta que para algo extraordinario podemos usar las matemáticas? ¡Venga! que si tú no vas a ser arquitecto no importa, aprender historia no está de más, que es cultura general.
La triangulación en el mundo
¿Y qué me dices de la NASA? Para comunicarse con las naves espaciales y cohetes; su código se basa en la lectura y análisis de la triangulación de las señales emitidas. Entonces, ahora dirás que ni que fueras a calcular la triangulación de los gritos de tu madre para utilizar en casa el Teorema de Pitágoras; pero calma, que existen muchas más aplicaciones.
¿Sabías que los móviles pueden rastrarse por triangulación? Ahora bien, al rastrear un móvil puedes rastrear a la persona que lo lleva. Así que venga, a darle las gracias a Pitágoras porque con base en su teorema podrás conseguir tu móvil si lo extravías; y hasta al novio si está perdido. Incluso, gracias a sistemas basados en geolocalización por triangulación es que las aseguradoras ubican coches abandonados o robados.
Parece que va tomando sentido esto de las matemáticas hasta este punto; pero todavía hay más. En tema de seguridad ciudadana también tenemos mucho que agradecer a Pitágoras; porque los geólogos detectan la actividad sísmica utilizando este teorema. Triangulando la distancia entre las ondas del sismo se puede determinar la intensidad del mismo; así como el centro del terremoto.
Además, los médicos forenses analizan la trayectoria de las balas utilizando el famoso teorema de Pitágoras. El sistema o coordenadas que rige todo lo que tiene que ver con dar en un blanco como misiles y otras armas están basados en este teorema. ¿Qué te parece? Y tú que creías que no tenía mucho sentido aprender sobre este tema.
Consejos
Para trabajos más rudimentarios como talar un árbol sin causar daño se puede utilizar el teorema de Pitágoras. Por ejemplo, si necesitamos talar un árbol de 16 metros; previniendo que la punta toque el suelo a 6 metros de la base, utilizando este teorema sabremos a qué altura debemos talar el árbol.
También, si necesitas cosechar frutos; pero no tienes una escalera, para construir una que te quede exacta, solo tienes que conocer la altura del árbol y la distancia que existe ente la base del árbol y el lugar dónde vas a ubicar la base de la escalera. Luego, simplemente aplicar el teorema de Pitágoras y listo: medida exacta.
En síntesis, podemos decir que el teorema de Pitágoras dice que en todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma del cuadrado de sus dos catetos. Esto es teoría chaval, que te toca ponerte creativo para encontrarle más aplicaciones de las que te hemos dado aquí.
Después de analizado estos casos, ahora podemos darnos cuenta que las matemáticas no son tan difíciles como parecen. Además, que son importantes y necesarias para nuestra vida. Si les dedicamos tiempo, esfuerzo y dedicación podremos verles siempre el lado positivo y hallar una manera de disfrutarlas.

