Cómo resolver ecuaciones
Contenido del Artículo
Antes de explicar cómo resolver ecuaciones, es necesario que sepas qué es una ecuación: es una igualdad que contiene incógnitas, términos y miembros. Definamos pues, cada uno de estos vocablos, para que no quedes con la idea en el tintero:
En primer lugar, una igualdad es una expresión que contiene el símbolo de igual (=). Las igualdades pueden ser numéricas y literales o algebraicas. Una igualdad numérica es aquella que contiene sólo números, por ejemplo: 2+3=5. Las igualdades literales o algebraicas son aquellas que contienen números y letras. Éstas a su vez pueden ser de dos tipos: identidades o ecuaciones.
Las identidades son aquellas ciertas para cualquier valor que se le dé a las incógnitas, ejemplo: Por el contrario, una ecuación es una igualdad que sólo es cierta para algunos valores de la o las incógnitas o variables.
Una incógnita, también llamada variable, es una letra cuyo valor se desconoce. Cabe destacar que las letras usadas como variables más frecuentemente son la x,y,w y z; sin embargo, cualquier letra es perfectamente usable como variable o incógnita.
Los términos, son cada una de las partes de la ecuación separados por los símbolos de + ó -.
Y por último, los miembros son cada una de las expresiones que están a cada lado de la ecuación, identificándose así dos miembros: el primer miembro, que es lo que se encuentra al lado izquierdo de la ecuación y el segundo término que es la expresión que se halla del lado derecho de la misma.
Partes de una ecuación
Fíjate en el siguiente ejemplo en el que se identifican cada una de las partes de una ecuación:
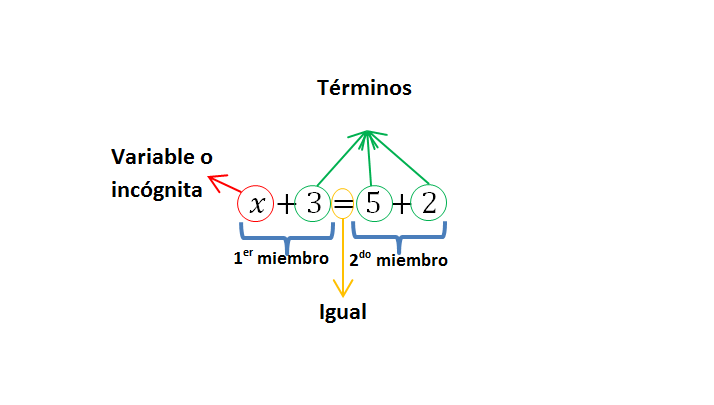
Importancia y función de las ecuaciones
Las ecuaciones son de gran importancia y uso en la vida cotidiana; aunque muchas veces no nos demos cuenta y no sea necesario plantear el problema de manera formal.
Por ejemplo, si vamos a adquirir un teléfono inteligente en nuestra tienda virtual preferida; y éste cuesta 500€, y contamos con 400€, es fácil saber que nos faltarían 100$ para comprar el producto. Pero, veamos cómo escribirlo en forma de ecuación: x+400€=500€
En este caso, sabemos que x=100, porque 100+400=500, pero en el caso de ecuaciones no tan fáciles de resolver ¿cómo procederíamos?
Instrucciones para resolver ecuaciones
Resolver una ecuación es hallar su solución, es decir, hallar el valor de la incógnita. Para ello es necesario conocer las propiedades de las igualdades, a saber:
- Si se suma o se resta un número a ambos lados de la igualdad, ésta no se altera.
- Si se multiplica o divide un número a ambos lados de la igualdad, esta no se altera.
Las ecuaciones se clasifican de acuerdo al exponente de la variable. En este apartado, estudiaremos ecuaciones de primer grado con una incógnita; también, ecuaciones de segundo grado con una incógnita.
Para poder resolver las ecuaciones de primer y segundo grado con una incógnita es necesario tener en cuenta las propiedades. Tanto de la adición como de la multiplicación en los conjuntos , a saber: propiedad asociativa, conmutativa, elemento neutro, elemento opuesto, factor cero y la propiedad distributiva del producto respecto a la adición.
También es necesario conocer la definición de términos semejantes. Que son aquellos que tienen la misma variable elevada al mismo exponente; y las reglas de los signos para la adición y la multiplicación.
Por último, es necesario conocer el orden de las operaciones. Esto es (si no hay signos de agrupación, sea paréntesis, corchetes y/o llaves): primero se resuelven potencias, luego multiplicaciones y divisiones y luego sumas y restas.
Ejercicios resueltos
Las ecuaciones de primer grado con una incógnita, son aquellas donde la variable tiene exponente 1 (el cual se sobreentiende).
Veamos algunos ejercicios:
X+2=5
- Para resolver una ecuación es necesario despejar la x. Esto quiere decir “dejarla sola” en alguno de los miembros de la igualdad; por lo general se deja sola del lado izquierdo.
- En este caso, para conseguirlo es necesario quitar el +2.
- Para ello, es necesario restarle 2. Esto con el fin de que al sumar o restar resulte cero, recordando la propiedad del elemento neutro para la adición: todo número sumado con cero resulta el mismo número.
- Así pues, al restarle 2 al primer miembro de la igualdad, que es donde se encuentra la variable, en este caso x, es necesario restarle también 2 al otro miembro de la igualdad para que ésta no se altere (recordando las propiedades de las desigualdades).
Veamos pues el procedimiento seguido para resolver esta ecuación:
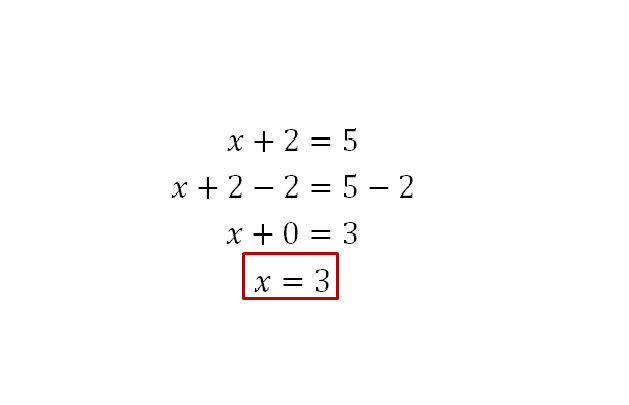
Como notaste, la variable tiene un valor de 3. Para saber si ese resultado es correcto, es necesario comprobar la ecuación. Comprobar una ecuación no es más que verificar si su resultado es correcto o no. Para ello, se deben seguir los siguientes pasos:
- Se sustituye o cambia la letra por el resultado
- Se resuelven las operaciones a cada lado de la igualdad SIN ALTERAR NINGÚN TÉRMINO.
- Si en cada miembro de la igualdad se observa el mismo valor, entonces el resultado de la ecuación es correcto, de lo contrario, no lo es.
Veamos cómo comprobar este ejercicio:
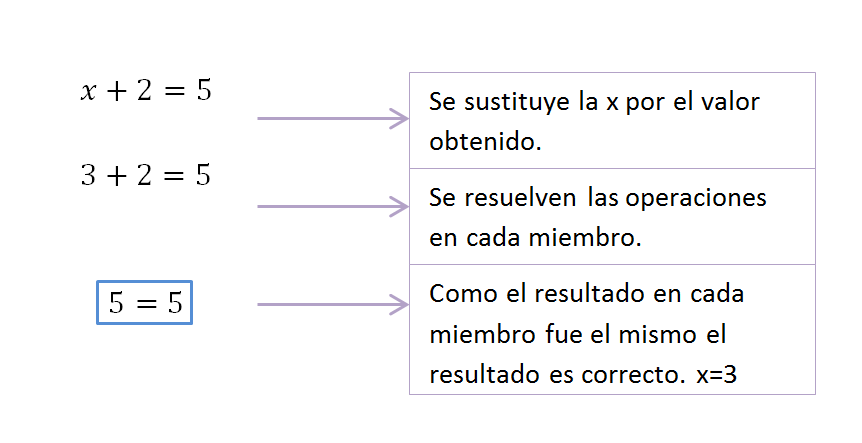
Para resolver este ejercicio: 3+y=7, se procede de manera similar que con el ejercicio anterior, sin importar si la variable, en este caso, se encuentra al comienzo o no de la ecuación:
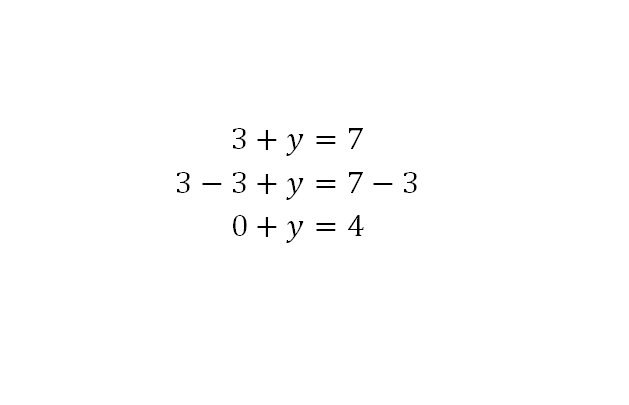
Comprobación:
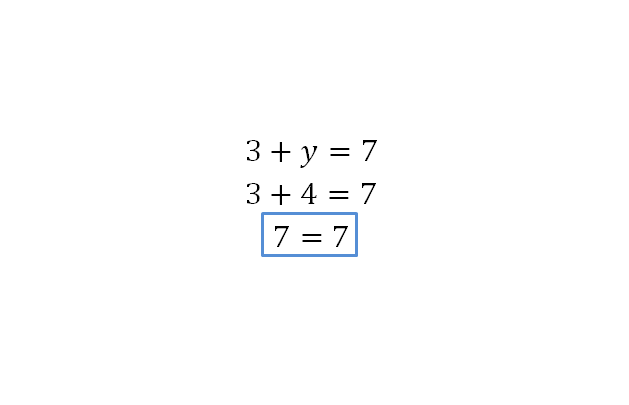
En este caso, veamos que del lado de la variable o incógnita no sólo hay que eliminar el número que resta, en este caso el 2, sino también hay un número que multiplica.
Para ello, se puede proceder eliminando primero cualquiera de los dos números, y luego, el siguiente, atendiendo nuevamente a las propiedades de las igualdades.
Nota que cuando no hay ningún signo entre un número y la variable o incógnita, se sobreentiende que está multiplicando a la variable. Generalmente y para facilitar los cálculos, se elimina primero el número que esté sumando o restando, en este caso, restando, así:
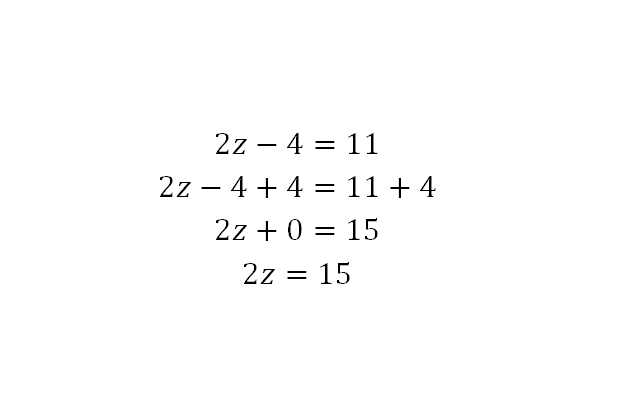
Como puede observarse, aún no se ha despejado la variable z. Para conocer su valor, es necesario eliminar el 2 que la está multiplicando. Para ello, se divide a ambos lados por el número 2 para que la igualdad nos se altere, esto con el fin de que al dividir un número por el mismo da como resultado 1 y, aplicando la propiedad del elemento neutro para la multiplicación: todo número multiplicado por 1 da como resultado el mismo número, entonces:
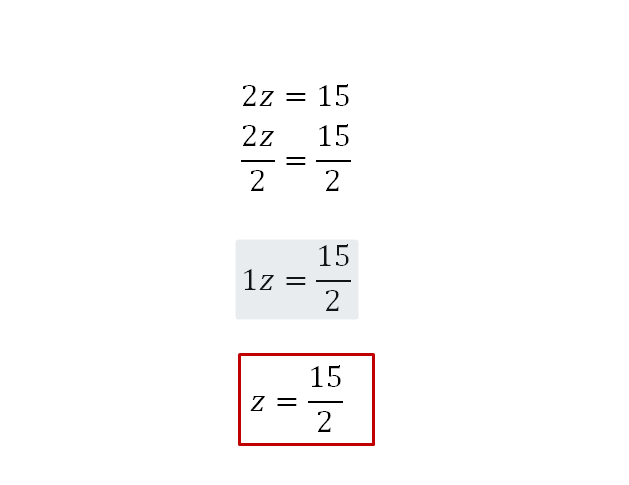
Fíjate que en este caso el resultado es una fracción. Se puede dar el resultado en forma de fracción o de manera decimal. En este caso el número decimal resultado de esta fracción es 7,5. Ahora, usaremos fracciones como soluciones.
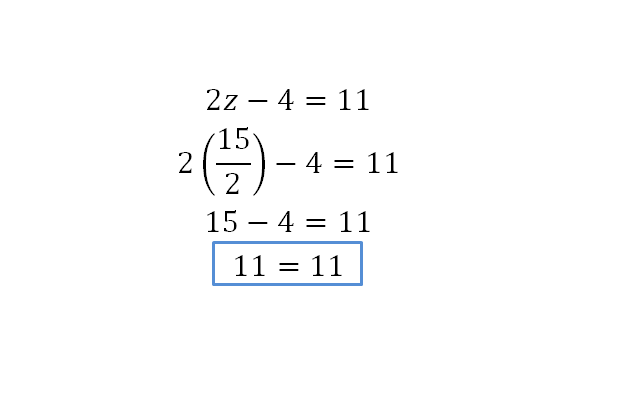 En este caso es necesario primero resolver la operación del lado derecho de la igualdad con el fin de simplificar operaciones, así:
En este caso es necesario primero resolver la operación del lado derecho de la igualdad con el fin de simplificar operaciones, así:
w/5+1=31+5
w/5+1=36
Luego, se procede como el ejercicio anterior, con la diferencia de que, en este caso se deben multiplicar ambos miembros de la igualdad por 5 con la finalidad de que nos e altere la igualdad.
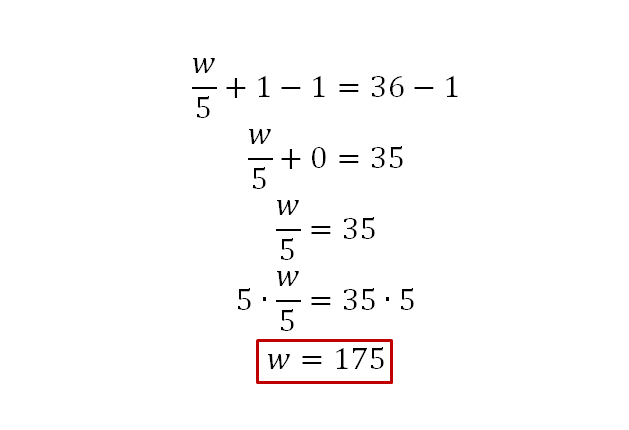
Comprobación:
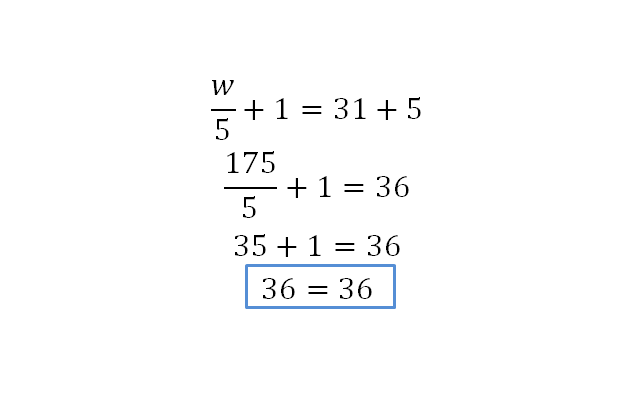
Para resolver este ejercicio: 2x+4=3x+1, como se observa la variable aparece más de una vez, te recomendamos primero colocar en un solo miembro los términos que contienen a la variable, y en el otro miembro los términos que no contienen la variable, es decir, agrupar términos semejantes, así:
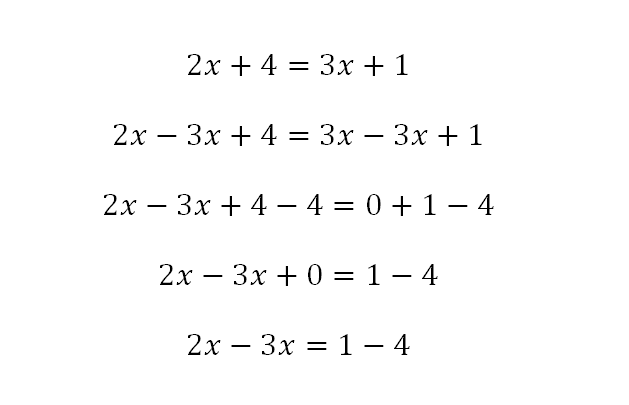
Ahora, procedamos a resolver las operaciones en ambos lados. Como 2x y 3x son términos semejantes se procede a operar normalmente, es decir, se resuelve la resta, atendiendo a la regla de los signos para la adición y se coloca la x, de esta forma:
2x-3x=1-4
-1x=-3
Luego, divide a ambos miembros de la igualdad por -1. Entonces, recordando las reglas de los signos para la multiplicación:

¿Que necesitas para resolver ecuaciones?
Para resolver de ecuaciones de segundo grado con una incógnita, es decir, ecuaciones donde la variable está elevada al exponente 2, es necesario conocer la fórmula de la resolvente, la cual viene dada por:
x=(-b±√(b^2-4ac))/2a
Fíjate que en la fórmula aparece el símbolo . Esto quiere decir que existirá un resultado para cuando se resuelva con + y otro para cuando se resuelva con -. Cuando√(b^2-4ac)=0 ambos resultados serán iguales, es decir, la ecuación tendrá una única solución.
La x es la variable que se desea despejar, la cual en este caso viene elevada al cuadrado, y las letras a, b y c, son los coeficientes de la variable y el término independiente. Así pues, esta fórmula es aplicable para despejar variables en ejercicios de la forma: ax2+bx+c=0
Lo que significa que basta con reducir las ecuaciones dadas a una expresión similar a ésta para poder aplicar la fórmula de la resolvente y obtener el valor de x.
En los casos de las ecuaciones de segundo grado, la x puede tener 1 solución, puede tener 2 soluciones y puede no tener solución.
Consejos para resolver ecuaciones
Para resolver ecuaciones de primer y segundo grado con una incógnita de forma más rápida y sencilla, se puede atender al concepto de ecuaciones equivalentes: dos ecuaciones son equivalentes si al resolverlas se obtiene el mismo resultado. Tomando esta definición y tratando de resumir las propiedades de las desigualdades, se podrían derivar las siguientes “reglas”:
- Lo que esté sumando en un miembro de la igualdad “pasa” al otro miembro restando.
- Lo que esté restando en un miembro de la igualdad “pasa” al otro miembro sumando.
- Lo que esté multiplicando en un miembro de la igualdad “pasa” al otro miembro dividiendo.
- Lo que esté dividiendo en un miembro de la igualdad “pasa” al otro miembro multiplicando.
De esta manera, resolvamos nuevamente el siguiente ejercicio, tomando en cuenta estas reglas:

Fíjate que se obtuvo el mismo resultado, resumiendo el número de pasos.
Una forma más sencilla de resolver algunas ecuaciones de segundo grado es tomando en cuenta los coeficientes de la variable, cuando ya se encuentra operada para poder aplicar la fórmula de la resolvente, es decir, de la forma: ax2+bx+c=0
Si a=0, podríamos entonces buscar 2 números que multiplicados den c y sumados den b. Es necesario tener en cuenta que no siempre estos números son fáciles de encontrar por mera inspección. Entonces, ya se aplicaría la fórmula de la resolvente como vimos anteriormente.
Veamos si se puede resolver de esta forma el ejercicio que resolvimos de ecuaciones de segundo grado:
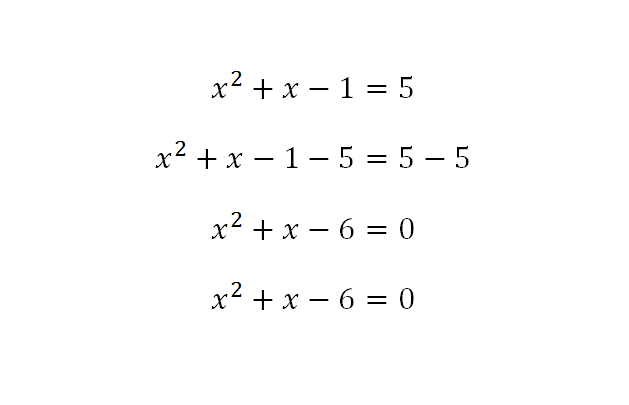
Dos números que sumados resulten -6, en este caso serían -3 y +2 ó +3 y -2. Ahora, dos números que multiplicados resulten 1, como es positivo y debemos escoger una de las dos opciones dadas, sería +3 y -.2, ya que 3-2=1. Entonces tenemos lo siguiente: (x+3)∙(x-2)=0
Luego, ambos números se igualan a 0 porque, de acuerdo a la propiedad del factor cero para la multiplicación, uno de los 2 factores debe ser 0 para que la igualdad sea cierta. Observarás que resultó lo mismo que aplicando la resolvente.
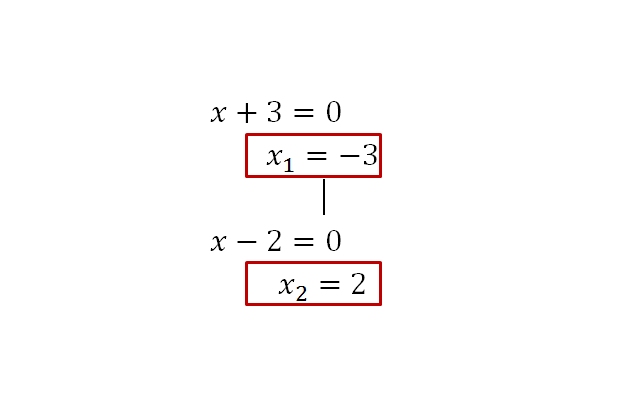


Busco otra opción ejemplo
Y=x+6
Como resuelvo
(+16)+21+(-3)
Está muy buena me ayudó muchísimo
como desarrollo x+35>47
agrdecere que me apoye en el desarrollo
x+35>47
Cómo calculo 12x+4=3x+5 /2
Como resolverx-1-2(x-5)=2x
Como resuelvo esto ×2-25=11
muy buena me ayudo un monton