Cómo convertir fracciones a decimales
Aunque parezca mentira, convertir fracciones a decimales es uno de los métodos matemáticos más usados y más útiles que existen, ya que se usa en infinidad de ocasiones.
Realmente un número decimal y una fracción es exactamente lo mismo, es decir la forma de representar a nivel matemático un número que no es entero. Por ejemplo, si un número tiene una parte no entera que es menos de la unidad, se puede añadir con decimal detrás de una coma o se puede representar en forma de fracción.
Lo que intento decir es que si tienes 4 parte de 1 y media parte de uno, puedes representarlo tanto como 4,5 como de la forma (4+1/2). De esta manera, vamos a poder usar los dos métodos para realizar cálculos.
Sin embargo, si has tenido matemáticas complejas, como por ejemplo las de bachillerato, te habrás dado cuenta que es mucho más fácil operar con fracciones que operar con números decimales. La razón es que las fracciones se calculan mejor, siempre tienen como resultados números enteros y quedan mucho más estéticas de vez.
Aparte que gracias a las fracciones, se pueden usar métodos para resolver problemas de matemáticas, como por ejemplo la descomposición factorial y la simplificación. Muchas veces nos encontramos un problema que si dejamos en decimales va a ser mucho más complicado de resolver que si tiene fracciones.
Este artículos para convertir decimales a fraciones seguro que también te interesa
Eso si, también hay ocasiones en las cuales esto es al revés, es decir, en las cuales necesitamos a los números decimales para poder hacer el problema. Realmente una fracción no es más que la representación vertical de una división, pero no es ningún número entero que podamos poner como resultado final.
Por este motivo, es necesario aprender a convertir una fracción a números decimales, ya que tan sólo así vamos a poder resolver algunos problemas complejos de matemáticas, al igual que ocurre al revés en algunas ocasiones.
La cosa es que seguramente seas una persona que al igual que yo, lleva muchos años ya sin estudiar matemáticas, ya que es algo que llevas sin dar desde el instituto y desde la universidad si eres de la rama de ciencias. Esto quiere decir que todo esto de las fracciones, los decimales y todo lo demás seguramente lo tengas un poco olvidado, es decir, que seguramente no lo sepas hacer ahora mismo.
Sin embargo, yo creo que el saber no ocupa lugar y que los conocimientos que tenías de matemáticas están por ahí en alguna parte. De esta manera, tan sólo necesitas a alguien que te refresque un poco la memoria, para que estos conocimientos vuelvan a salir otra vez a la vez.
Precisamente esto vamos a hacer en este artículo, en el cual vamos a aprender fácilmente y paso a paso como podemos convertir una fracción en decimales, para que puedas hacer operaciones matemáticas de la manera más sencilla posible.
Instrucciones para convertir fracciones a decimales
- Método 1, el método de la división:
El primer método que vamos a aprender en este artículo es el método de la división, método para convertir fracciones a decimales con el cual vamos a sacar muy rápidamente una operación de este tipo. La forma de hacerlo es bastante sencilla, ya que lo único que tenemos que hacer realmente es dividir el número de arriba de la fracción entre el número de abajo. De esta manera, el resultado que nos de va a ser el decimal de la fracción, el cual será el mismo que el resultado de la misma. Esto funciona bien porque realmente una fracción es una representación del decimal, pero en una forma de división que digamos que es un poco más agradable a la vista. Por ejemplo,es mucho más agradable a la vista poner 1/2 que poner 0,5, pero realmente es lo mismo. Este método es el más sencillo y el más eficaz, ya que si tenemos una calculadora a mano, lo vamos a poder hacer en cuestión de segundos.
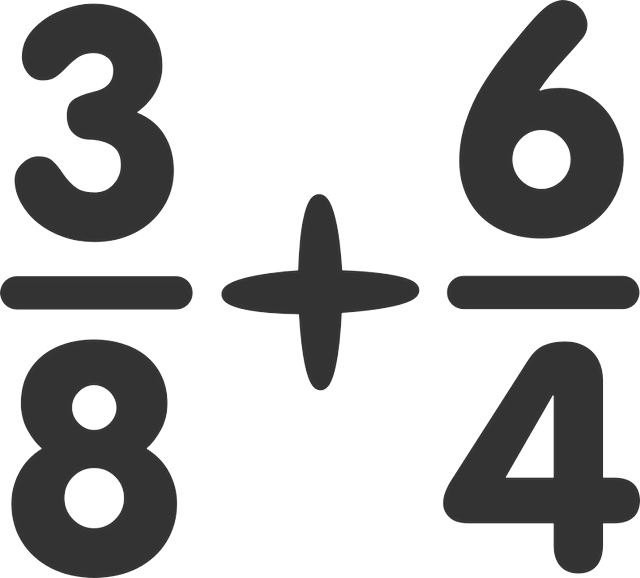
- Método 2: el método de la multplicación y la simplificación:
El segundo método que vamos a usar es el famoso método de la multiplicación y después la simplificación, un método que consiste en ver de una sola vez la parte de una fracción que ocupa con respecto a 100. Lo vamos a hacer con respecto a 100 ya que realmente los decimales son múltiplos de estos métodos. Después de hacerlo, vamos a dividir el número de arriba entre 100 para que nos de la forma decimal. La forma de hacerlo es dividir 100 entre el divisor de la fracción y luego coger ese número y multiplicarlo por este número. Una vez que sepamos cual es este número, multiplicamos también el número por el dividendo ya que de esta manera, el número no varía y se puede hacer la operación sin realizar ninguna alteración en el número en cuestión. Por ejemplo, si tenemos la fracción 1/4, dividimos 100/4 y nos da como resultado 25. Entonces multiplicamos 4×25 para tener un 100 y multiplicamos 25 x 1 para que nos de 25. De esta manera, tenemos la fracción 25/100 y si tenemos en cuenta que 100 es uno, 25 son 0,25, ya que 25/100 son 0,25. De esta manera, hemos conseguido lo mismo que en el paso 1, pero es algo que hemos podido hacer por nosotros mismos, sin tener que usar una calculadora. Por este motivo, este método te sacará de apuros en los casos en los cuales tengas fracciones complejas y no tengas calculadora a mano.

- Método 3: el método gráfico:
Este método es el que usaban los niños para aprender las fracciones, las cuales se dividían como trozos de algo, algo que hacía que fuera más divertido aprender y que por supuesto, fuera más fácil de aprender. Por ejemplo, si tenemos la fracción 1/4, vamos a trazar una línea en 4 partes iguales y vamos sólo a colorear una parte de ella. De esta manera, ya estamos sabiendo que sólo una parte de las 4 es una fracción. Ahora bien,cómo se pasa esto a un número, pues dividiendo la parte que hemos coloreado por la parte sin colorear, es decir 1/4 que son 0,25. Este método aunque no sea adecuado para un adulto, ya que como ves no sirve si tienes una calculadora, te puede servir para enseñar matemáticas de una forma sencilla a tus hijos, los cuales van a poder aprender con tan sólo un vistazo a los colores que hemos hecho.

- Método 4: el método » a ojo»:
Muchas veces hacemos cálculos de cosas que podemos hacer con la cabeza a ojo, sobre todo en fracciones sencillas. Por ejemplo, todo el mundo sabe que la mitad de algo es 0,5, así que si ves 1/2, que es la mitad de algo, vas a saber siempre que se trata de 0,5, sin sacar la calculadora ni nada de eso. En otros casos como 1/4, ocurre exactamente lo mismo, ya que si tratamos de dividir uno en 4 partes, nos queda la 0,25 parte de algo, es decir, 0,25 es el resultado de la operación. Como verás, no te hará falta calculadora nada más que en los casos más graves de fracciones, como por ejemplo 567/543, una fracción que no se puede resolver a ojo obviamente. Sin embargo, yo creo que hasta los múltiplos de 10 se pueden resolver a ojo sin problemas y sin usar ningún tipo de aparato para calcularlas.
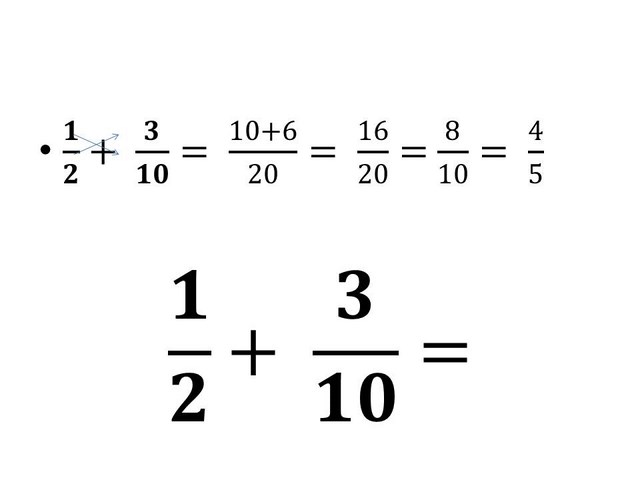


es muy bonito
es muy bonito
Buena info si pudiera le daría ★★★★★★★★★★ estrellas
No explican nada