Ejercicios y Problemas de Derivadas – Aprende las Derivadas
Contenido del Artículo
Lo primero que hay que entender, para poder realizar la derivada de una función, es el significado de la misma. En términos generales, una función se puede representar como una máquina, en la cual, existen unas incógnitas, que dependiendo del valor que le introduzcamos, nos dará otro valor, cómo, por ejemplo:
F(x)= x^2
- Si sustituimos x=1, nos devolverá, como valor y=1,
- si introducimos x=4, nos devolverá y= 16 y viceversa.
Todos esos valores se representan en una gráfica, que está compuesto por el eje de ordenadas (Y), y el eje de abscisas, (X). Una vez entendido esto, podemos entender más fácilmente la definición de una derivada.
Podemos definir la derivada de una función como: La pendiente de la recta tangente en un punto exacto de la gráfica, es decir, el estudio de la variación de la gráfica, en cada uno de sus puntos exactos.
Una vez entendido todo lo anterior, hay que conocer los pasos a seguir, para cada uno de los casos existentes, en los cuales se pueden aplicar las derivadas.
Para calcular la inclinación de una curva, bastaría con usar algunas técnicas de dibujo. Por ejemplo en la la curva que hace este dibujo [Curva «C»]. Es una línea dibujada en un diagrama muy popular, conocido como «sistema de coordenadas cartesianas», donde el eje horizontal se llama «abscisa» y el eje vertical se llama «ordenada». Si utilizamos un sistema cartesiano para pintar nuestra curva, tendremos más facilidades para calcular, el lugar concreto de cada punto de la línea curva.
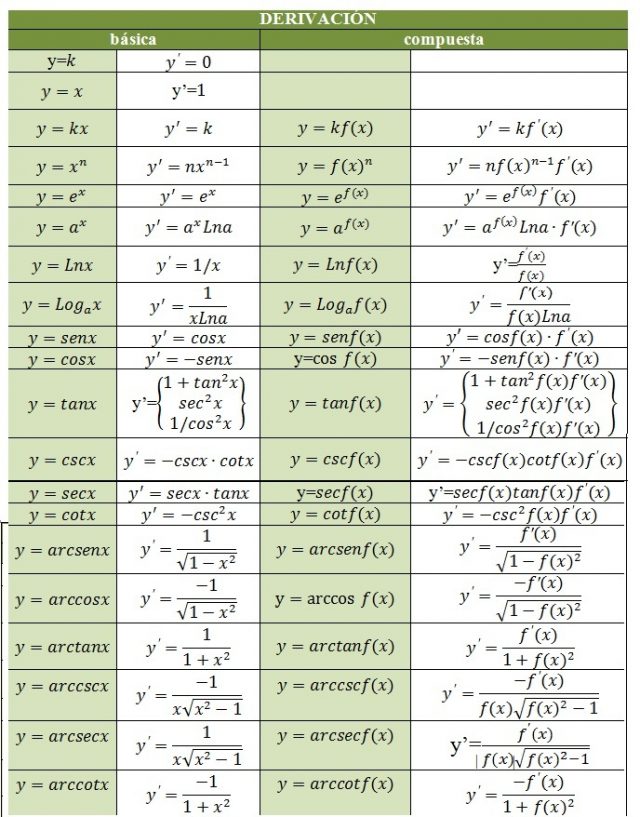
Explicación de la Tabla de derivación.
- Derivada de una constante es 0, y la función identidad es 1.
- Derivada de una función potencial con n perteneciente a los reales.
- La derivada de una función potencial simple, es igual al exponente multiplicado por su base menos una uno.
- La derivada de una función irracional simple, 1 partido por el índice de la raíz, por la propia raíz, con radicando n-1.
- La derivada de una fracción irracional simples, es igual a la expresión inversa del producto del índice, por la raíz del mismo índice, de la potencia n-1 del radicando x.
- La derivada de una función exponencial, es igual a la misma función, por el logaritmo neperiano de su base.
- La derivada de una función logarítmica, es igual 1, dividido por el producto de la incógnita, de la función logarítmica, por el logaritmo neperiano de su base.
- La derivada de la función exponencial potencial, es igual a la suma de las derivadas, de una función exponencial, y de una función potencial.
- La derivada del seno x, siempre es el coseno x.
- La derivada del coseno, es el – seno.
- La derivada de la función tangente, es igual a 1, más el cuadrado de la tangente.
- La derivada de la función arco seno, es igual a 1 dividido por la raíz cuadrada de 1 – x al cuadrado.
- La derivada de la función arco coseno, es igual a la derivada de la función arco seno, pero negada.
- La función arco tangente, es igual a 1 por 1 más x al cuadrado.
Para las funciones compuestas, se podrían resumir como, los pasos citados anteriormente, multiplicados por la derivada de la función que la contiene.
Es importante estudiarse esta tabla, para poder aplicar el uso de las derivadas, dependiendo del tipo de función que tengamos. Si no saben las fórmulas de cada derivada no se va a poder hacer ningún tipo de ejercicio o problema que las contenga. En el caso de que no se sepan de memoria, es recomendable que se imprima la tabla.
Operaciones con derivadas: (D= Derivada)
- Suma: D(f(x) + g (x)): D (f(x)) +D (g(x)) o también dicho la suma de dos funciones es igual a la suma particular de cada función.
- Resta: D(f(x) – g (x)) =: D (f(x)) -D (g(x)) para resumir fácilmente la resta de dos funciones es lo mismo que realizar la resta particular de cada una de las funciones.
- Multiplicación de funciones: D(f(x)*g(x)) =: D (f(x)) * g(x) + f(x) * D g(x) es decir, para realizar la derivada de una multiplicación se debe derivar la primera función y multiplicarla por la segunda sin derivar sumada por la primera función sin derivar multiplicada por la segunda función derivada.
- División de funciones: (D (f(x)) * g(x) – f(x) * D g(x)) g(x)^2.
Dicho de otro modo, se debe realizar la derivada de la primera función por la segunda función sin derivar restada por la primera función sin derivar multiplicada por la segunda función derivada y todo ello dividido por la segunda función elevada al cuadrado.
Propiedades de las funciones.
- Multiplicación de una constante K por una función: D (K*f(x)) = K* D (f(x))
- Regla de la cadena: D (f(g(x)) = D (f(g(x)) * D (g(x)) (Se basa simplemente en derivar la primera función y por consiguiente multiplicarla por la función que la compone)
Aprendida y entendida la teoría básica para el entendimiento y cálculo de las derivadas, pasaremos a realizar algunos ejercicios sencillos para su mejor comprensión a la hora de la practica:
Ejercicios y Problemas
Ejercicio número 1:
D [e- ²×] = e – ²× * -2.
Explicación: Esta función es de tipo exponencial compuesta, por lo que debemos dejar la misma función, multiplicada por la derivada de la función que tiene en su índice, que es menos dos, ya que la derivada de una función identidad es uno. Por lo tanto, menos dos por uno es menos dos.
D [ Ln ( 3ײ) * ( 5׳ -7)³] = D [ Ln ( 3ײ)] + D [3Ln( 5׳ -7)] = 6x/ 3ײ + 3 * 15ײ / 5׳ -7 = 2 / x + 45 ײ / 5׳ -7 =
10׳ – 14 + 45׳ / x (5׳ -7 )= 55׳ – 14 / x (5׳ -7 )
/ = La barra de la fracción, no es una división.
Explicación: Antes de realizar este ejercicio, se debe tener algunos conocimientos básicos, sobre las propiedades de los logaritmos:
- La multiplicación de logaritmos D [ Ln ( 3ײ) * ( 5׳ -7)³] es igual a la suma de las dos funciones que la contienen.
- . D[ Ln (3ײ)] + D [3Ln( 5׳ -7)]
- La división de logaritmos D [ Ln ( 3ײ )/ (5׳ – 7 )³)] es igual a la resta de las dos funciones que la contienen.
- D[ Ln (3ײ)] – D [3Ln( 5׳ -7)]
- Cualquier logaritmo de exponente” x” , por ejemplo , In (5׳ -7) ³ es igual al propio exponente , multiplicado por el logaritmo . 3 Ln ( 5׳ -7)
- El logaritmo de 0, no existe, y el logaritmo de 1 es 0.
- El logaritmo en base de a de a, es igual a 1.
- El logaritmo en base de n de a elevado a n, es igual a n.
- El logaritmo de los números negativos no existe, ya que el dominio de una función logaritmo, está comprendido para las x > 0.
- Una vez conocidas estas reglas, se opera las fracciones resultantes, de hacer las derivadas de los logaritmos de cada una de las funciones, y simplificamos el resultado obteniendo: . 60 ׳ -14 / x ( 5׳ -7).
Ejemplo número 2:
D [sen ( 2x) + cos (ײ)] = cos (2x )* 2 – sen (ײ) * 2x.
Explicación: La derivada de una suma como se ha explicado anteriormente se realiza, a través de las derivadas parciales de las funciones que se están sumando. Empezaremos derivando sen ( 2x) , que como sabemos al ser una función compuesta de una función seno, nos dará como resultado, por la derivada de la función que contiene 2x, obteniendo 2, ya que estamos realizando la derivada de una función identidad. Después pasaremos a derivar cos (ײ), que como sabemos, la derivada de una función compuesta de un coseno, es igual a – sen (ײ) , por la función que contiene, que en este caso nos encontramos con una función potencial, obteniendo así 2x cos (2x) * 2- sen (ײ) * 2x.
Ejemplo número 3:
/ = La barra de la fracción, no es una división.
D (arc tc 2x) = 2x * In 2 / 1 + 2² x
Explicación: Debido a que se trata de una función compuesta de una función arco tangente, atendiendo a la fórmula de la derivada de la arco tangente, se obtendría 1 / 1 + 2² x multiplicado por la derivada de la función que la contiene, tratándose de una función exponencial .2x * In2
Problema número 1:
Halla las ecuaciones de las rectas tangente y normal a la curva y = 2׳ + x en el origen de coordenadas.
F (x) = +2׳ x.
- La ecuación de la recta tangente es : y –y1 = m ( x –×1 ).
Explicación: Debido a que el problema pide, las ecuaciones de las rectas situadas en el origen de coordenadas, el valor de x = 0, por lo tanto, sustituiremos f (x) por f (0), obteniendo como valor 0. Una vez realizado este paso, se deberá operar la derivada de f (0) que es 6 * 0² + 1 = 1.
Recta tangente: y – f(0) = f´(0) * (x-0) = f´(x) =6ײ + 1 = f´(0) =1
Y – 0 = 1 (x-0) = y=x.
- La ecuación de la recta normal es: y1 – = 1/D y1 ( x –x1 ).
Explicación: Como se ha explicado anteriormente, se seguirán los mismos pasos, excepto por la pendiente m, que es lo que nosotros señalamos como -1 / f´ (0) , operando como hemos hecho anteriormente, obtendríamos como resultado:
Y – 0 = -1 (x – 0) = y = -x.
Recta normal: y-f(0)= -1 / fx (0) * (x -0)
/ = La barra de la fracción, no es una división.
Problema número 2
Halla los valores de a y b para los cuales la recta tangente a la curva y=ײ + a x + b en el punto P (3,0) tenga de pendiente 2.
La gráfica de la curva dada, pasa por el punto P (3,0) = 0 =9 +3a+b.
Debido a que nos dan los puntos, x= 3 e y= 0, deberemos sustituirlos en la función dada, obteniendo como resultado el indicado abajo, y además realizaremos a la derivada de la misma, para poder así, hallar el valor de a, y por consiguiente el valor de b:
F´ (3) = 2 = como f´(x) =2x + a = f´ (3) = 6 + a = 6 + a= 2 = a = -4
Por lo tanto, a = -4 Y b =-9 – 3ª = 3 = a= -4 y b =3

